МОЖНО НЕ ВСЕ ВОПРОСЫ, НО ХОТЯ БЫ 4 ШТУКИ Под деревом Тумтум завёлся Бармаглот. У Бармаглота 2020 голов. На бой с Бармаглотом
Вышел рыцарь. У рыцаря есть 4 типа разящих мечей, которые могут отрубить только
определённое количество голов. У Бармаглота есть весьма странная система регенерации,
позволяющая ему мгновенно отращивать головы. Перечислим разящих мечей, с
учётом регенерации голов Бармаглота: если отрубить ему 33 головы, то вырастет 40 голов; если
отрубить 21 голову, то не вырастет ни одной; если отрубить 17 голов, то вырастет 14; если
отрубить 1 голову, то вырастет 10.
1. Можно ли отрубить ему все головы? Если да, то как?
2. Какое наименьшее количество ударов мечами надо сделать, чтобы отрубить все головы?
3. Как данными мечами срубить все головы, если голов 2021? Какое наименьшее количество
ударов придется сделать?
4. Как данными мечами срубить все головы, если голов 1? Какое наименьшее количество ударов
придется сделать?
5. Для любого ли натурального Hможно убить Бармаглота с Н головами, если у рыцаря есть
описанный набор мечей?
6. Пусть тєN, neNo{0}. Назовём меч (т, п)-разящим, если он может срубить т голов и при этом
вырастает п голов. Можно ли подобрать набор из трёх (т, п)-разящих мечей (ут — n| > 2) с
которых можно убить Бармаглота с любым натуральным количеством голов? Если
можно, то опишите все такие тройки разящих мечей.
7. Предложите свои обобщения. В качестве одного из обобщений можно рассмотреть случай,
когда у Бармаглота есть еще и хвосты, которые тот может использовать как некое оружие. В этом
случае следует предусмотреть возможность отрубать хвосты Бармаглоту по каким-то правилам,
аналогичным отрубаниям голов.

Показать ответ

Ответ:

Данииб

15.08.2022 18:11

S=155,61 дм²

Пошаговое объяснение:

S¹-общая площадь длина×высота

S²-общая площадь длина×ширина

S³-общая площадь ширина×высота

S-общая площадь

Цифрами:

1)6,6÷2=3,3 дм-1 ребро (например ширина)

2)4,5÷2=2,25 дм-1 ребро (например высота)

3)75,6-3,3×4-2,25×4=53,4 дм-учетверённое число

4)53,4÷4=13,35 дм-1 ребро (например длина)

5)13,35×2,25×2=60,075 дм²-S¹

6)13,35×3,3×2=88,11 дм²-S²

7)3,3×2,25×2=7,425 дм²-S²

8)60,075+88,11+7,425=155,61 дм²-S

ответ:S=155,61 дм².

Буквами:

a-длина

b-ширина

c-высота

1)6,6÷2=b

2)4,5÷2=c

3)4(a+b+c)-b×4-c×4=4a

4)4a÷4=a

5)a×c×2=S¹

6)a×b×2=S²

7)b×c×2=S³

8)S¹+S²+S³=S

0,0(0 оценок)

Ответ:

Шекспир112005

15.07.2021 00:51

Что мы будем использовать: последовательность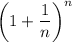 $\left(1+\dfrac{1}{n}\right)^n$ монотонно возрастает и имеет конечный предел; этот предел обозначается буквой e. Первые цифры числа e все знают. Для нас достаточно знать, что

$2\le(1+\frac{1}{n})^n$

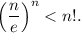1) $\left(\dfrac{n}{e}\right)^n$ При n=1 неравенство очевидно. Предположим, что оно справедливо при некотором n, и докажем, что тогда оно справедливо при n+1. Итак, нужно доказать, что 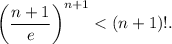$\left(\dfrac{n+1}{e}\right)^{n+1}$ Имеем:

$(\frac{n+1}{e})^{n+1}=(\frac{n}{e})^n\cdot (\frac{n+1}{n})^n\cdot\frac{n+1}{e}$

2)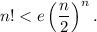 При n=1 неравенство очевидно. Предположив, что при некотором n неравенство справедливо, докажем, что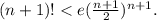 (n+1)!

Имеем:

$(n+1)!=n!\cdot (n+1)$

$e\frac{(n+1)^{n+1}}{2^n}\cdot \dfrac{1}{(1+\frac{1}{n})^n}\le e\frac{(n+1)^{n+1}}{2^n}\cdot \frac{1}{2}=e(\frac{n+1}{2})^{n+1}.$

Доказательство завершено благодаря тому, что все натуральные числа расположены "по порядку" одно за другим, и есть первое натуральное число (принцип домино: если доминошки расположить на боку одну рядом с другой на небольшом расстоянии друг от друга в виде змеи, и уронить первую доминошку на вторую, то вторая упадет на третью, третья на четвертую и так далее, пока не упадут все).

0,0(0 оценок)

Популярные вопросы: Математика