Объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
У правильной шестиугольной призмы основанием является правильный шестиугольник, где боковые грани перпендикулярны основаниям.
Объем правильной шестиугольной призмы равен произведению площади правильного шестиугольника, лежащего в основании, на высоту призмы, где высота призмы - это её боковое ребро.
У нас боковое ребро равно 10 см, а ребро основания равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
см3.
Правильная шестиугольная призма имеет два основания, где ее основания - правильные шестиугольники со стороной , и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами и .
Поэтому площадь полной поверхности правильной шестиугольной призмы равна сумме площадей ее двух оснований и шести площадей боковых граней призмы.
Где площадь основания находится согласно формуле:
А площадь боковых граней равна:
Подставляя это в формулу общей площади получим:
Подставляя наши значения получаем:
см2.
Получаем ответ: объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Рассмотрим сложенный из дощечкек квадрат на листочке в клеточку и увидим, что:
а - большая сторона параллелограмма,
а - основание маленького треугольника,
а - боковое ребро среднего треугольника
2а - основание большого треугольника,
b - меньшая сторона параллелограмма,
b - сторона маленького квадрата,
b - сторона маленького треугольника,
2b - основание среднего треугольника
2b - боковое ребро большого треугольника.
Посчитаем периметры отдельных фигур:
1) периметр большого треугольника:
2а + 2b + 2b = 2a + 4b
2) периметр среднего треугольника:
а + а + 2b = 2a + 2b
3) периметр маленького треугольника:
b + b + a = 2b + a
4) периметр маленького квадрата:
4b
5) периметр параллелограмма:
2а + 2b.
Теперь рассмотрим сложную фигуру.
Итак:
1) слева внизу большой треугольник, из периметра которого надо исключить меньшую сторону параллелограмма:
2а + 4b - b = 2a + 3b
2) на основании большого треугольника расположены параллелограмм, из которого имеют значение только две стороны а и b, и маленький треугольник, из которого имеет значение только боковая сторона b
a + b + b = a + 2b
3) из маленького квадрата в центре фигуры имеет значение только две стороны b:
Но поскольку заданная сложная фигура симметрична, несмотря на то, что ее левая и правая стороны сложены из разных фигур, мы можем учесть только одну сторону маленького квадрата b, найти периметр половины сложной фигуры и умножить на 2.
Объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Пошаговое объяснение:
У правильной шестиугольной призмы основанием является правильный шестиугольник, где боковые грани перпендикулярны основаниям.
Объем правильной шестиугольной призмы равен произведению площади правильного шестиугольника, лежащего в основании, на высоту призмы, где высота призмы - это её боковое ребро.
У нас боковое ребро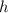 равно 10 см, а ребро основания
равно 10 см, а ребро основания  равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
равно 4 см (как наглядно показано на рисунке). Подставляем и считаем:
Правильная шестиугольная призма имеет два основания, где ее основания - правильные шестиугольники со стороной , и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами
, и шесть боковых сторон, которые представляют из себя прямоугольники со сторонами  и
и 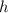 .
.
Поэтому площадь полной поверхности правильной шестиугольной призмы равна сумме площадей ее двух оснований и шести площадей боковых граней призмы.
Где площадь основания находится согласно формуле:
А площадь боковых граней равна: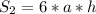
Подставляя это в формулу общей площади получим:
Подставляя наши значения получаем:
Получаем ответ: объем полной поверхности правильной шестиугольной призмы равен 415,7 см3, а площадь 323,1 см2.
Рассмотрим сложенный из дощечкек квадрат на листочке в клеточку и увидим, что:
а - большая сторона параллелограмма,
а - основание маленького треугольника,
а - боковое ребро среднего треугольника
2а - основание большого треугольника,
b - меньшая сторона параллелограмма,
b - сторона маленького квадрата,
b - сторона маленького треугольника,
2b - основание среднего треугольника
2b - боковое ребро большого треугольника.
Посчитаем периметры отдельных фигур:
1) периметр большого треугольника:
2а + 2b + 2b = 2a + 4b
2) периметр среднего треугольника:
а + а + 2b = 2a + 2b
3) периметр маленького треугольника:
b + b + a = 2b + a
4) периметр маленького квадрата:
4b
5) периметр параллелограмма:
2а + 2b.
Теперь рассмотрим сложную фигуру.
Итак:
1) слева внизу большой треугольник, из периметра которого надо исключить меньшую сторону параллелограмма:
2а + 4b - b = 2a + 3b
2) на основании большого треугольника расположены параллелограмм, из которого имеют значение только две стороны а и b, и маленький треугольник, из которого имеет значение только боковая сторона b
a + b + b = a + 2b
3) из маленького квадрата в центре фигуры имеет значение только две стороны b:
Но поскольку заданная сложная фигура симметрична, несмотря на то, что ее левая и правая стороны сложены из разных фигур, мы можем учесть только одну сторону маленького квадрата b, найти периметр половины сложной фигуры и умножить на 2.
Найдем периметр сложной фигуры:
1) 2а + 3b + a + 2b + b = 3a + 6b = 3(a + 2b) - полупериметр сложной фигуры.
2) 2 • 3(a + 2b) = 6(a + 2b) или 6а + 12b
ответ: 6(a + 2b) или 6а + 12b.