т.к. у нас два сундук с четным количеством монет и два с нечетным, а за операцию каждый сундук меняет свою четность, то всегда будет два "нечетных" сундука
так как на одной итерации мы добавляем в три из четырех сундуков монеты, то только в одном сундуке мы можем добиться 0
значит, с учетом двух утверждений картина с наибольшим количеством монет могла выглядеть следующим образом: 0 1 1 1108
на предыдущем шаге должно было быть 3 0 0 1107 - но такого быть не могло, согласно утверждениям выше
следующий вариант, где монет меньше, чем 1108, это 1107
этого варианта достичь можно, пользуясь следующим алгоритмом:
четвертый сундук не трогаем, а с остальными повторяем следующую операцию:
берем сундук с наибольшим количеством монет и проводим операцию столько раз, сколько нужно, чтобы в сундуке осталось меньше трех монет
2) 120 уч.
3) 90 очков
4) 40 уч.
Пошаговое объяснение:
Первая задача.Кр.запись.
250 руб - было всего
120 руб - потратила
? - часть своих денег Маша заплатила за мороженое
Решение.
120 / 250 =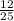
- Маша заплатила за мороженое
Вторая задача.Кр. запись.
420 уч. - всего
? уч. - ходят в муз. школу, но сказано, что ходят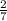
от всего кол-ва
Решение.
420 *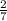
= 420 : 7 * 2 = 120 уч. - ходят в муз. школу
Третья задача.Кр. запись.
24 очка - получил капитан
? очков - получила команда, но сказано, что капитан получил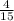
всех полученных очков.
Решение.
24 :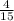
= 24 * 
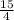= 24 : 4 * 15 = 90 очков - получила команда
Четвёртая задача.Кр.запись
в 3 классах поровну учащихся
? уч. - в каждом классе, но сказано, что если в каждый класс добавить по 3 уч., то всего в них будет 129 уч
Решение.
3 * 3 = 9 уч. - добавили
129 - 9 = 120 уч. - в 3 классах
120 : 3 = 40 уч. - в каждом классе.
1107
Пошаговое объяснение:
т.к. у нас два сундук с четным количеством монет и два с нечетным, а за операцию каждый сундук меняет свою четность, то всегда будет два "нечетных" сундука
так как на одной итерации мы добавляем в три из четырех сундуков монеты, то только в одном сундуке мы можем добиться 0
значит, с учетом двух утверждений картина с наибольшим количеством монет могла выглядеть следующим образом: 0 1 1 1108
на предыдущем шаге должно было быть 3 0 0 1107 - но такого быть не могло, согласно утверждениям выше
следующий вариант, где монет меньше, чем 1108, это 1107
этого варианта достичь можно, пользуясь следующим алгоритмом:
четвертый сундук не трогаем, а с остальными повторяем следующую операцию:
берем сундук с наибольшим количеством монет и проводим операцию столько раз, сколько нужно, чтобы в сундуке осталось меньше трех монет
выглядит это так:
111 222 333 444
222 333 0 555
333 0 111 666
0 111 222 777
74 185 0 851
135 2 61 912
0 47 106 957
35 82 1 992
62 1 28 1019
2 21 48 1039
18 37 0 1055
30 1 12 1067
0 11 22 1077
7 18 1 1084
13 0 7 1090
1 4 11 1094
4 7 2 1097
6 1 4 1099
0 3 6 1101
2 5 0 1103
3 2 1 1104
0 3 2 1105
1 0 3 1106
2 1 0 1107
и он возьмет себе 1107 монет