Тогда не существует и аналогичных конфигураций "строго левее и строго выше" и так далее, потому что если бы они были, мы бы могли их поворотами доски или отражениями привести к конфигурации "строго правее и строго выше"
Значит координаты любых двух фишек на нашей доске не могут быть обе различными. Значит фишки максимум занимают одну вертикаль и одну горизонталь, но так можно разложить лишь 199 фишек. А у нас 200. Значит, мы получаем противоречие исходному предположению.
Переформулируем. Пусть дано 200 пар чисел: , причем каждое из чисел взято в отрезке . Требуется доказать, что найдутся две пары чисел и , такие что и (по сути, — координаты фишки на доске).
Доказательство:
Предположим обратное. Расставим пары по убыванию первого числа (то есть числа ). Внутри групп с одинаковым первым числом проведем обратную операцию: расставим числа по возрастанию второго числа (). Например, если размеры доски , а расставлено 7 фишек, то подошла бы следующая расстановка:
Понятно, что такая расстановка возможна. Действительно, если это не так, то найдется число , причем число стоит выше числа . Это противоречит предположению.
Пусть — число переходов числа на более низкое (в вышеприведенном примере таких переходов 3: с 4 на 3, с 3 на 2, с 2 на 1). Заметим, что числа могут повторяться не более одного раза. Внутри групп они строго возрастают. Поэтому последнее число не меньше . При этом, очевидно, . С другой стороны, переходов не больше чем (спуск от 100 до 1). Противоречие, которое завершает доказательство.
Допустим таких конфигураций не существует.
Тогда не существует и аналогичных конфигураций "строго левее и строго выше" и так далее, потому что если бы они были, мы бы могли их поворотами доски или отражениями привести к конфигурации "строго правее и строго выше"
Значит координаты любых двух фишек на нашей доске не могут быть обе различными. Значит фишки максимум занимают одну вертикаль и одну горизонталь, но так можно разложить лишь 199 фишек. А у нас 200. Значит, мы получаем противоречие исходному предположению.
Переформулируем. Пусть дано 200 пар чисел: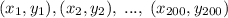 , причем каждое из чисел взято в отрезке
, причем каждое из чисел взято в отрезке ![[1,\; 100]](/tpl/images/1360/3515/a94ff.png) . Требуется доказать, что найдутся две пары чисел
. Требуется доказать, что найдутся две пары чисел 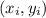 и
и 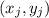 , такие что
, такие что 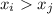 и
и 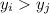 (по сути,
(по сути, 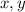 — координаты фишки на доске).
— координаты фишки на доске).
Доказательство:
Предположим обратное. Расставим пары по убыванию первого числа (то есть числа ). Внутри групп с одинаковым первым числом проведем обратную операцию: расставим числа по возрастанию второго числа (
). Внутри групп с одинаковым первым числом проведем обратную операцию: расставим числа по возрастанию второго числа (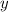 ). Например, если размеры доски
). Например, если размеры доски 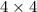 , а расставлено 7 фишек, то подошла бы следующая расстановка:
, а расставлено 7 фишек, то подошла бы следующая расстановка:
Понятно, что такая расстановка возможна. Действительно, если это не так, то найдется число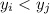 , причем число
, причем число 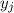 стоит выше числа
стоит выше числа 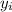 . Это противоречит предположению.
. Это противоречит предположению.
Пусть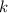 — число переходов числа
— число переходов числа  на более низкое (в вышеприведенном примере таких переходов 3: с 4 на 3, с 3 на 2, с 2 на 1). Заметим, что числа
на более низкое (в вышеприведенном примере таких переходов 3: с 4 на 3, с 3 на 2, с 2 на 1). Заметим, что числа 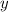 могут повторяться не более одного раза. Внутри групп они строго возрастают. Поэтому последнее число не меньше
могут повторяться не более одного раза. Внутри групп они строго возрастают. Поэтому последнее число не меньше 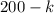 . При этом, очевидно,
. При этом, очевидно, 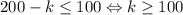 . С другой стороны, переходов не больше чем
. С другой стороны, переходов не больше чем 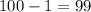 (спуск от 100 до 1). Противоречие, которое завершает доказательство.
(спуск от 100 до 1). Противоречие, которое завершает доказательство.