На доске выписаны все натуральные числа от 1 до 19 без пропусков и повторений: 1,2,. оля играет в арифметическую игру: за один ход она выбирает два из написанных на доске чисел и записывает на доске модуль их разности увеличенный на 2, а сами выбранные числа стирает. так она продолжает до тех пор, пока на доске не останется только одно число. может ли на доске остаться 1) 19 2) 18.

Показать ответ

Ответ:

danilcoptsov1

30.03.2023 18:20

ответ: нельзя

Пошаговое объяснение:

1)2020-1=2019. Разделим на 2 кучки 5+2014

2)2014-1=2013. уже есть 3 кучки 5+5+2008 (забираем из бОльшей)

3) 2008-1=2007. Теперь 4 кучки 5+5+5+2002 (забираем из бОльшей)

Как мы видим, каждый раз большая кучка уменьшается на 6 камней (5 переложили и 1 выкинули) Значит, начальное число должно быть кратным 6-ти, тогда все кучки будут по 5 камней.

делимость на 6: четное число+сумма цифр длится на 3.

2020-четное, но сумма цифр 2+2=4. Значит, число не кратно 6-ти, значит, условие не может быть выполнено.

0,0(0 оценок)

Ответ:

valeria8002

03.08.2021 03:13

-10

Пошаговое объяснение:

Нам тут понадобится правило Лопиталя.

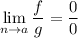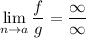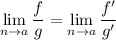
если $\displaystyle \lim_{n \to a} \dfrac fg=\dfrac00$ или $\displaystyle \lim_{n \to a} \dfrac fg=\dfrac\infty\infty$ то $\displaystyle \lim_{n \to a} \dfrac fg=\displaystyle \lim_{n \to a} \dfrac {f'}{g'}$

$\displaystyle \lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(x-1)}{\arccos(x-1)\cdot(x^2-2x+1)}$

2 Вынесем -1 по формуле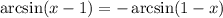 $\arcsin(x-1)=-\arcsin(1-x)$

$\displaystyle -\lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(1-x)}{\arccos(x-1)\cdot(x^2-2x+1)}$

3 Запишем предел произведения дробей как произведение пределов

$\displaystyle- \lim_{x \to 1} \frac{1}{\arccos(x-1)}\cdot\lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(1-x)}{x^2-2x+1}$

4 Подставим в первом пределе значение и посчитаем

$\displaystyle- \lim_{x \to 1} \frac{1}{\arccos(1-1)}\cdot\lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(1-x)}{x^2-2x+1}$

$\displaystyle-\lim_{x \to 1}\frac{1}{\arccos0}\cdot\lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(1-x)}{x^2-2x+1}$

$\displaystyle-\dfrac2\pi\cdot\lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(1-x)}{x^2-2x+1}$

5 Cоберем квадрат в знаменателе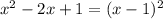 x^2-2x+1=(x-1)^2

$\displaystyle-\dfrac2\pi\cdot\lim_{x \to 1} \frac{\sin(5\pi x)\cdot\arcsin(1-x)}{(x-1)^2}$

6 Получили предел вида $\dfrac00$ воспользуемся правилом Лопиталя

$\displaystyle-\dfrac2\pi\cdot\lim_{x \to 1} \frac{(\sin(5\pi x)\cdot\arcsin(1-x))'}{(x-1)'}$

$\displaystyle-\dfrac2\pi\cdot\lim_{x \to 1} \frac{\sin(5\pi x)'\cdot\arcsin(x-1)+\sin(5\pi x)\cdot\arcsin(1-x)'}{2x-2}$

$\displaystyle-\dfrac2\pi\cdot\lim_{x \to 1} \frac{(-x(x-2))^{-\frac12}\bigg(5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)-\sin(5\pi x) \bigg)}{2x-2}$

Тут я сразу вынес за скобки

7 Вынесем $\dfrac12$ (взял 2 в знаменателе) за предел и сократим

$\displaystyle-\dfrac1\pi\cdot\lim_{x \to 1} \frac{(-x(x-2))^{-\frac12}\bigg(5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)-\sin(5\pi x) \bigg)}{x-1}$

8 Распишем как произведение пределов

$\displaystyle-\dfrac1\pi\cdot\lim_{x \to 1}(-x(x-2))^{-\frac12}\cdot \lim_{x \to 1} \frac{5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)-\sin(5\pi x)}{x-1}$

9 Посчитаем первый предел

$\displaystyle-\dfrac1\pi\cdot\lim_{x \to 1}(-1(1-2))^{-\frac12}\cdot \lim_{x \to 1} \frac{5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)-\sin(5\pi x)}{x-1}$

$\displaystyle-\dfrac1\pi\cdot1\cdot \lim_{x \to 1} \frac{5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)-\sin(5\pi x)}{x-1}$

10 Распишем разность дробей в пределе

$\displaystyle-\dfrac1\pi\cdot \lim_{x \to 1} \frac{5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)}{x-1}-\frac{\sin(5\pi x)}{x-1}$

11 Распишем предел разности как разность пределов

$\displaystyle-\dfrac1\pi\cdot \Bigg(\lim_{x \to 1} \frac{5\pi\sqrt{-x(x-2)}\arcsin(1-x)\cos(5\pi x)}{x-1}-\lim_{x \to 1}\frac{\sin(5\pi x)}{x-1}\Bigg)$

12 Распишем первый предел как произведение пределов и вынесем 5π

$\displaystyle-\dfrac1\pi\cdot \Bigg(5\pi\lim_{x \to 1}\sqrt{-x(x-2)}\cos(5\pi x)\lim_{x \to 1}\frac{\arcsin(1-x)}{x-1}-\lim_{x \to 1}\frac{\sin(5\pi x)}{x-1}\Bigg)$

13 Посчитаем первый предел

$\displaystyle-\dfrac1\pi\cdot \Bigg(5\pi\lim_{x \to 1}\sqrt{-1(1-2)}\cos(5\pi )\lim_{x \to 1}\frac{\arcsin(1-x)}{x-1}-\lim_{x \to 1}\frac{\sin(5\pi x)}{x-1}\Bigg)$