Покажем, что последняя цифра не может быть двойкой. Действительно, если это так, то пусть . Тогда , но поскольку эти числа отличаются лишь последней цифрой (и 2>0), то , противоречие.
Это был один из начать рассуждение, которое, однако, вряд ли к чему либо приведет.
Рассмотрим другой подход. Заметим, что . Пусть исходное число построено так: . Пусть . Тогда , противоречие. Аналогично доказывается для любой позиции двойки в числе, кроме второй слева. Идея состоит в том, что вычитаемое четырехзначное число достает таким образом до позиции, которая остается в числе, а значит, нарушает равенство. Остается лишь сделать так, чтобы эта позиция исчезала. Собственно, поставить двойку на вторую позицию
Теперь рассмотрим вычитание столбиком:
, откуда ясно, что , или , но два быть не может, поскольку у нас ровно одна двойка, или , наконец или .
1. надо продифференцировать числитель и знаменатель и потом вычислить предел, производная числителя равна 12х+13, а знаменателя 6х+8, можно еще раз продифференцировать числитель и знаменатель, , в числителе получим 12, в знаменателе 6, значит, предел равен 12/6=2 2.Ко второму примеру применить правило Лопиталя нельзя, т.к. предел отношения двух бесконечно малых величин должен быть равен пределу отношения их производных, если последний предел существует, но это не так. предел не существует.
3. найдем производные числителя и знаменателя, а потом возьмем предел при х стремящемся к к нулю. (2cos2х)/(2sin2x)=ctg2x, а
Покажем, что последняя цифра не может быть двойкой. Действительно, если это так, то пусть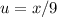
. Тогда 
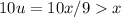, но поскольку эти числа отличаются лишь последней цифрой (и 2>0), то 
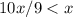, противоречие.
Это был один из начать рассуждение, которое, однако, вряд ли к чему либо приведет.
Рассмотрим другой подход. Заметим, что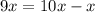
. Пусть исходное число построено так: 
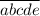. Пусть 
. Тогда ![\overline{abced}=9\times \overline{abed}=\overline{abed0}-\overline{abed}\leq \overline{a[b-1]ed0}](/tpl/images/1428/2431/04d5d.png)
, противоречие. Аналогично доказывается для любой позиции двойки в числе, кроме второй слева. Идея состоит в том, что вычитаемое четырехзначное число достает таким образом до позиции, которая остается в числе, а значит, нарушает равенство. Остается лишь сделать так, чтобы эта позиция исчезала. Собственно, поставить двойку на вторую позицию
Теперь рассмотрим вычитание столбиком:
Получаем два числа: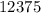
и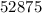 
.
1. надо продифференцировать числитель и знаменатель и потом вычислить предел, производная числителя равна 12х+13, а знаменателя 6х+8, можно еще раз продифференцировать числитель и знаменатель, , в числителе получим 12, в знаменателе 6, значит, предел равен 12/6=2 2.Ко второму примеру применить правило Лопиталя нельзя, т.к. предел отношения двух бесконечно малых величин должен быть равен пределу отношения их производных, если последний предел существует, но это не так. предел не существует.
3. найдем производные числителя и знаменателя, а потом возьмем предел при х стремящемся к к нулю. (2cos2х)/(2sin2x)=ctg2x, а
предел ctg2x, если х устремить к нулю, равен ∞