На клетчатом поле 7 ×
7 в левой верхней клетке находится робот. В остальных клетках поля записаны различные буквы. Робот умеет шагать в соседнюю клетку по вертикали вниз или по горизонтали вправо. Покидая клетку, робот стирает записанную в ней букву и записывает ее себе в память. Как только робот доходит до клетки "Запись", он записывает результат в компьютер. Вам необходимо составить алгоритм для робота, результатом работы которого будет запись слова "ГИПЕРССЫЛКА" в память компьютера.

Робот управляется с команд, которые записываются цифрами 1 и 2. Каждая из этих цифр обозначает следующее:

1 - Шагнуть вправо по горизонтали на 1 клетку.

2 - Шагнуть вниз по вертикали на 1 клетку.

Вам необходимо записать последовательность команд (последовательность цифр из 1 и 2), выполняя которые робот сможет записать в память компьютера слово "ГИПЕРССЫЛКА".

Выходить за пределы поля робот не может. В случае, если роботу поступает команда, которая выводит его за пределы поля, он игнорирует ее.

Пошаговое объяснение:

Пусть Джо поставит вначале 1 доллар. Если выиграет, пусть он скажет "хорошо" и снова поставит 1 доллар. Если проиграет, то в следующей ставке он ставит 2 доллара. Если он выигрывает, то его выигрыш покроет предыдущий проигрыш, и по сумме двух ставок он выиграет 1 доллар. После этого пусть Джо снова скажет "хорошо" и в новой ставке ставит 1 доллар. Если он проиграет и во второй раз, в третий раз он поставит 4 доллара, чтобы в случае выигрыша покрыть предыдущие проигрыши. Если проигрывает в третий раз, то в четвертый раз ставит 8 долларов, если проигрывает и в четвертый, то в пятый раз ставит 16 долларов. По условию он не проигрывает пять раз подряд, значит играя таким образом до первого выигрыша, он заработает 1 доллар не более, чем за 5 ставок. После этого он скажет "хорошо" и будет ставить также, как вначале.

Итак, после 1000 "хорошо" Джо выиграет 1000 долларов. Для этого ему потребуется сделать не более 5000 ставок.

10. У нас дано, что A⊂B.

Докажем, что (C\B)⊂(C\A).

Доказательство.

Пусть x∈C\B, тогда x∈C и x∉B,

если x∉B, то (т.к. A⊂B) x∉A, имеем

x∈C и x∉A, => x∈C\A.

чтд.

11. Доказательство "⇒".

Пусть у нас дано (A∪B = A∩B), докажем тогда, что A = B.

Доказательсво. Пусть x∈A, тогда x∈AUB, но т.к. A∪B = A∩B, то

x∈A∩B, и т.к. A∩B⊂B,  имеем x∈B. Мы доказали сейчас, что А⊂B.

Теперь докажем, что B⊂A. Доказательство аналогичное:

пусть x∈B, => x∈A∪B, т.к. A∪B = A∩B, то x∈A∩B, т.к. A∩B⊂A, => x∈A.

Итак, B⊂A.

Т.к. A⊂B и B⊂A, ⇔ A = B. чтд.

Доказательство "<=".

Пусть у нас дано A = B, докажем тогда, что A∪B = A∩B.

Если A = B, то A∪B = B∪B = B, и A∩B = B∩B = B,

то есть A∪B = B = A∩B.

чтд.

12. Доказательство "=>"

Пусть у нас дано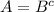 , докажем тогда, что

(A∩B = ∅) и (A∪B = U).

Доказательство. это по определению есть U\B, где U - универсальное множество, то есть у нас дано

A = U\B, тогда

A∩B = (U\B)∩B,

если x∈A∩B, то x∈A и x∈B, то есть x∈U\B и x∈B, то есть

x∈U и x∉B, и x∈B,

x не может одновременно и принадлежать B и не принадлежать B, то есть такого x не существует, то есть x∈∅, мы доказали, что A∩B ⊂∅, но тогда A∩B = ∅.

теперь докажем, что A∪B = U,

Очевидно, что A∪B ⊂U,

докажем, что U⊂A∪B (при условии ).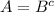

если x∈U, тогда x∈B или x∉B,

( если x∉B, тогда x∈ ), имеем

x∈B или x∈

но т.к.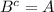

имеем

x∈B или x∈A, то есть

x∈A∪B.

Мы доказали, что U⊂A∪B, и что A∪B⊂U (очевидное утверждение)

Итак, A∪B = U.

Доказательство "<=".

Пусть у нас дано: (A∩B = ∅) и (A∪B = U). Докажем, что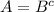

Доказательство. Пусть x∈A, при этом возможны два варианта:

x∈B или x∉B, то есть x∈B или x∈.

Если x∈B, тогда имеем x∈A∩B = ∅⊂

либо же x∈ и x∈A, ⇔ x∈A∩ ⊂,

то есть если x∈A => x∈

Пусть x∈, тогда x∈U\B, что значит x∈U и x∉B,

но т.к. U = A∪B, то имеем x∈A∪B и x∉B, то есть имеем

(x∈A или x∈B) и x∉B

если x∈A и x∉B, ⇔ x∈A\B ⊂ A, => x∈A,

если же x∈B и x∉B, то x∈∅ ⊂A, то есть x∈A,

итак ⊂A.

Мы доказали, что   A⊂, и

.

чтд.