На координатном луче росположены точки A(-- дробь одна вторая) B(0.2) C(дробь три четвертых) D(--0.6)Упорядочите отрезки по увеличению их длины. AC AB BD BC CD
Сначала нужно перенести все неизвестные члены уравнения в одну сторону, а известные в другую.
Неизвестные это члены с переменными (х,y,a,b и т.д.)
При переносе знаки меняются, то есть если было х = 1, то будет х -1 = 0
Знак изменился у 1 с +1 на -1. (просто знак + перед числами принято не писать)
У нас получится: х - 8х = - 14
Или можно сделать так: 14 = 8x -x
Переносить можно в обе стороны, главное следить за знаком. Обычно делают так, что бы неизвестное было слева, но т.к. у нас все отрицательное, мы перенесем его вправо.
Мы имеем уравнение: 14 = 8x -x
Для удобства можно поменять их местами и получиться 8х - х = 14.
Теперь нужно привести подобные. У подобных слагаемых одинаковые буквенные части. То есть, если бы у нас было 2x+8y-2y+8x = 2х+8х+8y-2у = 10х + 6у
В нашем случае будет 8х - х = 7х.
(Если стоит просто х, то это можно считать как 1х, что бы было проще. И получается 8х - 1х = 7х. 8-1=7 и просто дописываем х)
Значит все уравнение будет иметь вид 7х = 14
Теперь, что бы найти х нужно поделить правую часть на основание при Х.
Тоесть поделить 14 на 7
х =
х = 2.
Теперь проверим. Подставим 2 вместо Х в изначальное уравнение.
1) Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
2) Чтобы разделить дробь на натуральное число, надо делимое умножить на число, обратное делителю.
3) Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель — число, находящееся в нижней части дроби, числитель — в верхней), нужно сложить их числители, а знаменатель оставить тем же.
4) Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.
5) Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.
6) Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
Сначала нужно перенести все неизвестные члены уравнения в одну сторону, а известные в другую.
Неизвестные это члены с переменными (х,y,a,b и т.д.)
При переносе знаки меняются, то есть если было х = 1, то будет х -1 = 0
Знак изменился у 1 с +1 на -1. (просто знак + перед числами принято не писать)
У нас получится: х - 8х = - 14
Или можно сделать так: 14 = 8x -x
Переносить можно в обе стороны, главное следить за знаком. Обычно делают так, что бы неизвестное было слева, но т.к. у нас все отрицательное, мы перенесем его вправо.
Мы имеем уравнение: 14 = 8x -x
Для удобства можно поменять их местами и получиться 8х - х = 14.
Теперь нужно привести подобные. У подобных слагаемых одинаковые буквенные части. То есть, если бы у нас было 2x+8y-2y+8x = 2х+8х+8y-2у = 10х + 6у
В нашем случае будет 8х - х = 7х.
(Если стоит просто х, то это можно считать как 1х, что бы было проще. И получается 8х - 1х = 7х. 8-1=7 и просто дописываем х)
Значит все уравнение будет иметь вид 7х = 14
Теперь, что бы найти х нужно поделить правую часть на основание при Х.
Тоесть поделить 14 на 7
х =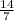
х = 2.
Теперь проверим. Подставим 2 вместо Х в изначальное уравнение.
2 = 8*2 - 14
2 = 16 - 14
2 = 2.
Решение верное.
1) Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.
2) Чтобы разделить дробь на натуральное число, надо делимое умножить на число, обратное делителю.
3) Для того чтобы сложить дробные выражения с одинаковым знаменателем (знаменатель — число, находящееся в нижней части дроби, числитель — в верхней), нужно сложить их числители, а знаменатель оставить тем же.
4) Для того чтобы вычесть от одного дробного выражения второе (с одинаковым знаменателем), нужно вычесть их числители, а знаменатель оставить тем же.
5) Для того чтобы сложить или вычесть дробные выражения с разными знаменателями, нужно найти наименьший общий знаменатель.
6) Для того чтобы найти дробное произведение, нужно перемножить числители и знаменатели, при этом, если есть возможность, сократить.
Примеры:
1) 1/3:5/8=1/3*8/5=8/15
5/7:9/3=5/7*3/9=15/63=5/21
2) 5/4*5=5/4*1/5=1/4=0,25
4/6:9=4/6*1/9=4/54=2/27
3) 5/6+1/6=6/6=1
2/3+5/3=7/3=2 1/3
4) 5/8/4/8=1/8=0,125
8/2-1/2=7/2=3 1/2=3,5
5) 5/8-6/1=5/8-48/8=-43/8=-5 3/8
1/5+4/6=6/30+20/30=26/30=13/15
6) 6/5*1/2=3/5=0,6
2/5*1/4=1/10=0,1
Вроде всё, удачи с учёбой.