Далее заметим, что для любого верно . То есть верхнее ограничение выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Пошаговое объяснение:
Введем замену
; 
.
Уравнение примет вид
Далее заметим, что для любого
верно 
. То есть верхнее ограничение 
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения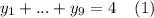 
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов
y = 3xe^x
1. Найти область определения функции.
2. Исследовать поведение функции на концах области определения. Найти точки разрыва
функции и ее односторонние пределы в этих точках. Найти вертикальные асимптоты.
3. Найти точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.
4. Найти наклонные асимптоты графика функции.
6. Найти точки экстремума и интервалы возрастания и убывания функции.
7. Найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
8. Построить график функции, используя все полученные результаты.
Пошаговое объяснение: