а) Таблица отношения (никогда таким не занимался, думаю, она должна выглядеть примерно так):
1 | 2 | 3 | 4
1 * | | | *
2 | * | * |
3 | * | * |
4 * | | | *
Область определения — X = {1, 2, 3, 4}. Область значений — Y = {1, 2, 3, 4}.
б) Отношение рефлексивно, т. к. : есть пары (1; 1), (2; 2), (3; 3), (4; 4).
Отношение не антирефлексивно, т. к.
Отношение симметрично, т. к. : (1; 4) — (4; 1), (2; 3) — (3; 2) + все пары вида (x; x).
Отношение не антисимметрично, т. к. : (2; 3) и (3; 2).
Отношение транзитивно, т. к. : (1; 1), (1; 4) — (1; 4); (1; 4), (4; 4) — (1; 4); (1; 4), (4; 1) — (1; 1); (4; 1), (1; 4) — (4; 4). Аналогично с 2 и 3.
в) P является отношением эквивалентности, т. к. рефлексивно, симметрично, транзитивно. P не является отношением порядка, так как не антисимметрично.
Отношение не является функцией, т. к. , например, (1; 1), (1; 4).
а) Таблица отношения (никогда таким не занимался, думаю, она должна выглядеть примерно так):
1 | 2 | 3 | 4
1 * | | | *
2 | * | * |
3 | * | * |
4 * | | | *
Область определения — X = {1, 2, 3, 4}. Область значений — Y = {1, 2, 3, 4}.
б) Отношение рефлексивно, т. к.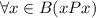
: есть пары (1; 1), (2; 2), (3; 3), (4; 4).
Отношение не антирефлексивно, т. к.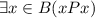
Отношение симметрично, т. к.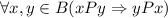
: (1; 4) — (4; 1), (2; 3) — (3; 2) + все пары вида (x; x).
Отношение не антисимметрично, т. к.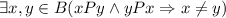
: (2; 3) и (3; 2).
Отношение транзитивно, т. к.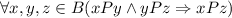
: (1; 1), (1; 4) — (1; 4); (1; 4), (4; 4) — (1; 4); (1; 4), (4; 1) — (1; 1); (4; 1), (1; 4) — (4; 4). Аналогично с 2 и 3.
в) P является отношением эквивалентности, т. к. рефлексивно, симметрично, транзитивно. P не является отношением порядка, так как не антисимметрично.
Отношение не является функцией, т. к.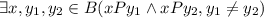
, например, (1; 1), (1; 4).