На окружности отмечено 2020 точек. Лягушонок прыгает с одной отмеченной точки на другую, двигаясь по часовой стрелке. За один прыжок он может перепрыгнуть через 99 или через 100 отмеченных точек. Сможет ли лягушонок побывать во всех отмеченных точках ровно по одному разу и вернуться в ту же точку, с которой стартовал?
Пусть лягушонок стартует в точке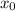 . Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке
. Тогда, если какие-то две точки повторились, то лягушонок побывал также в точке 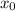 дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение
дважды, т.е. мы попали в цикл. Если мы покажем, что уравнение 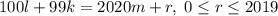 имеет решение при любом
имеет решение при любом  , то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку
, то цикл будет состоять из всех точек, и лягушонок побывает во всех точках по одному разу, а затем вернется в точку 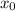 ;
;
Докажем для начала, что если существует решение для остатков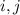 , то существует решение для остатка
, то существует решение для остатка 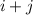 . Это вполне очевидно: просто сложим два уравнения для остатков
. Это вполне очевидно: просто сложим два уравнения для остатков 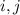 . Теперь, в частности, если существует решение для
. Теперь, в частности, если существует решение для 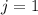 , то существует решение для всех остатков. То есть нам надо решить диофантово уравнение
, то существует решение для всех остатков. То есть нам надо решить диофантово уравнение 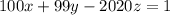 ; Для этого сразу положим
; Для этого сразу положим 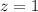 ; Пусть
; Пусть 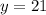 ;
;
Тогда из числа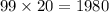 нам нужно получить число
нам нужно получить число 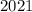 ; Но мы умеем прибавлять единицу:
; Но мы умеем прибавлять единицу: 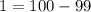 . То есть
. То есть 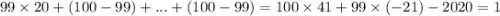 ; Иными словами, получили решение
; Иными словами, получили решение 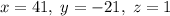 , но нам нужно решение в натуральных числах. Не вопрос: добавим к
, но нам нужно решение в натуральных числах. Не вопрос: добавим к 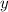 2020, а к
2020, а к  добавим 99. Получим решение:
добавим 99. Получим решение: 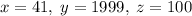 .
.
Итак, план действий следующий.
Пусть мы находимся в точке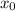 . Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке
. Прыгаем 41 раз на 100 и 1999 раз на 99. Теперь мы в точке 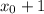 . Таким образом, мы посетим все точки.
. Таким образом, мы посетим все точки.