На острове рыцарей и лжецов 1000 посёлков. В каждом посёлке живут либо только рыцари, либо только лжецы. Некоторые посёлки соединены дорогами, при этом от любого посёлка можно добраться до любого другого. Жители каждого из посёлков сделали два утверждения:
От нашего посёлка ведут дороги хотя бы в три других посёлка.
От нашего посёлка ведут дороги хотя бы в два посёлка лжецов.
Какое наименьшее количество дорог может быть на острове?
Это значит, что его надо представить в виде суммы двух чисел, одно из которых составляет 2 равных части, а другое - 7 таких же частей.
Можно решать по действиям:
1) 2 + 7 = 9 - всего равных частей в числе 513.
2) 513 : 9 = 57 - приходится на одну часть
3) 57 · 2 = 114 - первое число
4) 57 · 7 = 399 - второе число
513 = 114 + 399, причем 114 : 399 = 2 : 7
Можно решать с уравнением:
пусть х - одна часть,
тогда 2х - первое число,
7х - второе число.
2x + 7x = 513
9x = 513
x = 57, а дальше те же действия 3) и 4)
Высота цилиндра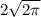 см.
см.
Боковая поверхность цилиндра см².
см².
Пошаговое объяснение:
Дано: цилиндр, осевое сечение ABCD, площадь осевого сечения S(ABCD) = 16 см², площадь основания Sосн = 8 см².
Найти: высоту цилиндра H, площадь боковой поверхности цилиндра Sбок.
Решение.
Осевым сечением цилиндра называется сечение, проходящее через ось цилиндра. Оно представляет собой прямоугольник, две стороны которого образующие цилиндра, а две другие - диаметры оснований цилиндра.
На чертеже OD = R - радиус основания, AD =2R - диаметр основания, CD = H - высота цилиндра.
1) Зная площадь основания (площадь круга), найдем радиус и диаметр основания:
Sосн = πR² = 8 см². ⇒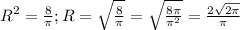 ;
;
Диаметр основания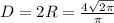 ;
;
2) Площадь сечения цилиндра - это площадь прямоугольника ABCD.
S(ABCD) = AD * CD = D * H = 16 см².
Высота цилиндра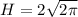 см.
см.
3) Боковая поверхность цилиндра равна произведению длины окружности основания на высоту цилиндра.
Длина окружности основания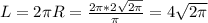 ;
;
Sбок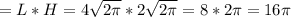 см².
см².