На плоскости отмечено 100 точек, никакие три из которых не лежат на одной прямой. Некоторые пары точек соединены отрезками. Известно, что никакая тройка отрезков не образует треугольника. Какое наибольшее число отрезков могло быть проведено?
Пусть всего точек. Рассмотрим граф на этих вершинах. Рассмотрим вершину (пусть это вершина ) с наибольшей степенью. Пусть эта степень равна . Заметим, что у вершин, имеющих связь с нет ребер к другим вершинам, связанным с (иначе получился бы треугольник). Поэтому степень этих вершин не больше, чем . Степени оставшихся не превосходят . Поэтому сумма степеней не превосходит . Количество ребер не превосходит (последнее неравенство — следствие из н-ва между ср. арифм. и ср. геометр.)
С другой стороны, несложно привести пример: рассмотрим двудольный граф (две равные доли по 50 вершин) и проведем всевозможные ребра (их будет 50*50=2500).
Если же проведено более 2500 ребер, то образуется хотя бы один треугольник (на самом деле их будет хотя бы 50).
Пусть всего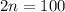 точек. Рассмотрим граф на этих вершинах. Рассмотрим вершину (пусть это вершина
точек. Рассмотрим граф на этих вершинах. Рассмотрим вершину (пусть это вершина 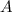 ) с наибольшей степенью. Пусть эта степень равна
) с наибольшей степенью. Пусть эта степень равна  . Заметим, что у вершин, имеющих связь с
. Заметим, что у вершин, имеющих связь с 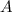 нет ребер к другим вершинам, связанным с
нет ребер к другим вершинам, связанным с 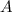 (иначе получился бы треугольник). Поэтому степень этих вершин не больше, чем
(иначе получился бы треугольник). Поэтому степень этих вершин не больше, чем  . Степени оставшихся не превосходят
. Степени оставшихся не превосходят  . Поэтому сумма степеней не превосходит
. Поэтому сумма степеней не превосходит 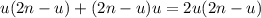 . Количество ребер не превосходит
. Количество ребер не превосходит 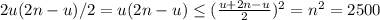 (последнее неравенство — следствие из н-ва между ср. арифм. и ср. геометр.)
(последнее неравенство — следствие из н-ва между ср. арифм. и ср. геометр.)
С другой стороны, несложно привести пример: рассмотрим двудольный граф (две равные доли по 50 вершин) и проведем всевозможные ребра (их будет 50*50=2500).
Если же проведено более 2500 ребер, то образуется хотя бы один треугольник (на самом деле их будет хотя бы 50).
ответ: 2500