На рисунке изображены 2 игрушки: мишка и котик.высота мишки 20 см.найдите примерную высоту котика в см

Показать ответ

Ответ:

dachapetruchka

12.12.2020 22:12

Ни одна фея не скажет про себя, что она лжет.
На 4-ый вопрос все должны были ответить "Да". Значит, фей всего 100.
Теперь рассмотрим первые 3 вопроса, про платья.
Те, кто лгут, на два вопроса ответят "Да" и на один правильный "Нет".
Говорящие правду, наоборот, на один вопрос ответят "Да" и на два "Нет".
Из правдивых фей пусть х носят красное платье, у желтое и z розовое.
Из лгущих фей пусть u носят красное платье, v желтое и w розовое.
На вопрос: Ты носишь красное платье? 30 сказали "да" и 70 "нет".
x + v + w = 30
y + z + u = 70
На вопрос: Ты носишь желтое платье? 50 сказали "да" и 50 "нет".
y + u + w = 50
x + z + v = 50
На вопрос: Ты носишь розовое платье? 70 сказали "да" и 30 "нет".
z + u + v = 70
x + y + w = 30
Получаем следующее:
{ x + v + w = 30
{ x + y + w = 30
Отсюда y = v, т.е. из фей в желтом 1/2 лгут и 1/2 говорят правду.
У нас есть уравнение:
x + z + v = 50
Подставляем
x + z + y = 50
Но это и есть суммарное количество правдивых фей.
ответ: 50

0,0(0 оценок)

Ответ:

katyamarkova22

22.09.2020 07:36

$a\in(-\infty, a_0)\cup(a_0,0)\cup(0,1/4)$ , где $a_0\approx-0.16$

Пошаговое объяснение:

В числителе стоит квадратный трёхчлен, у него может быть не более 2 корней. Значит, чтобы у уравнения было ровно 2 различных корня, числитель должен иметь 2 корня, и ни один из корней числителя не должен быть корнем знаменателя.

У числителя два неравных корня, если дискриминант больше нуля:

D=1-4a0

Найдём, при каких a хотя бы какой-то корень числителя является корнем знаменателя:

$x^2-x+a=x^2-2x+a^2-6a=0\\\begin{cases}x=a^2-7a\\x^2-x+a=0\end{cases}$

Подставляем найденный x в уравнение:

$a^2(a-7)^2-a(a-7)+a=0\\a(a^3-14a^2+49a-a+7+1)=0\\a(a^3-14a^2+48a+8)=0$

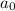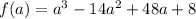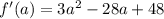Один корень (a = 0) находится легко, еще один корень можно выписать по формулам для кубических уравнений или найти графически. Можно показать, что что этот корень a_0 единственный и удовлетворяет неравенству 1 - 4a > 0: производная функции f(a)=a^3-14a^2+48a+8 равна f'(a)=3a^2-28a+48 . При a < 1/4 производная положительна, кроме того, 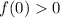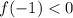f(0)0 , f(-1)<0 , поэтому f(a) имеет корень на отрезке [-1, 0]. Выражение для 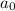a_0 довольно-таки громоздкое, по графику $a_0\approx-0.16$