. На рисунке показан график, представляющий 36 результатов анализа простых производителей. Мы называем эту диаграмму простым деревом анализа производителей. Есть ли у этого графика цикл? Есть ли у этого графа вершина, не связанная с другими? Составьте такой график для следующих чисел: а)48 б)96. в)24.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна . По теореме умножения
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна . По теореме умножения:
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна . По теореме умножения :
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна . По теореме умножения:
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна . По теореме умножения:
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна . По теореме умножения
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна . По теореме умножения:
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна . По теореме умножения :
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна . По теореме умножения:
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна . По теореме умножения:
Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна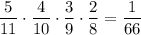 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна 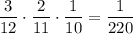 . По теореме умножения
. По теореме умножения 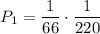
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна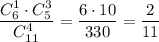 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 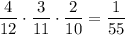 . По теореме умножения:
. По теореме умножения: 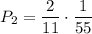
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: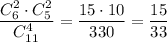 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 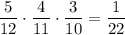 . По теореме умножения :
. По теореме умножения : 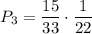
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна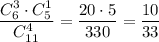 . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна 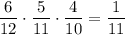 . По теореме умножения:
. По теореме умножения: 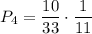
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: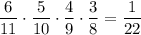 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 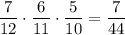 . По теореме умножения:
. По теореме умножения: 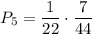
Итого, по теореме сложения:
Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна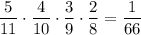 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна 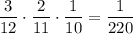 . По теореме умножения
. По теореме умножения 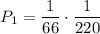
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна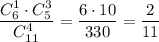 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 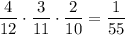 . По теореме умножения:
. По теореме умножения: 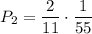
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: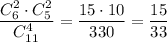 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 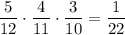 . По теореме умножения :
. По теореме умножения : 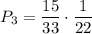
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна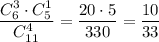 . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна 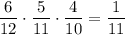 . По теореме умножения:
. По теореме умножения: 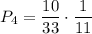
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: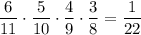 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 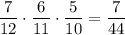 . По теореме умножения:
. По теореме умножения: 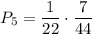
Итого, по теореме сложения: