На рисунке внутри прямоугольника, дан квадрат. ответьте на вопросы 1 и 2. 2 дм 14 см 10 см 1. Найдите площадь краевой части. А) 180 см B) 192 см C) 162 см D) 172 см 2. Найдите длину всех сторон закрашенной части фигуры А) 10 дм 2 см В) 9 дм 8 см C) 10 дм 8 см D) 9 дм 6 см
1) Сумма последовательных десяти чисел — это сумма членов арифметической прогрессии с разностью 1. Пусть первый член равен a. Тогда сумма a, a + 1, ... , a + 9 равна , а стёртый член равен . Стёртый член должен быть не меньше первого члена прогрессии и не больше последнего:
Рассмотрим десять последовательных чисел, начиная с 218 (218, 219, ... , 227). Их сумма равна 10 * 218 + 45 = 2225. Стёртый член равен 2225 - 2002 = 223. Он содержится в последовательности, так как 218 < 223 < 227. Значит, ответ верный.
2) В первом стакане количество воды увеличилось в 1,01 * 1,02 * ... * 1,27 раз. Во втором стакане количество воды увеличилось в 1,27 * 1,26 * ... * 1,01. Множители в этих произведениях равны, значит, оба произведения равны. Количество воды в обоих стаканах увеличилось в одинаковое количество раз.
Перед нами - линейное неоднородное ДУ 2 порядка с постоянными коэффициентами и с правой частью "специального" вида f(x)=e^(m*x)*[P1(x)*cos(n*x)+P2(x)*sin(n*x)], где m=3, n=0, P1(x)=8, P2(x)=0. Его решение y(x)=y1+y2, где y1 - общее решение однородного ДУ y"-2*y'+y=0, а y2 - частное решение данного неоднородного ДУ.
1) Найдём y1. Составляем характеристическое уравнение (ХУ): k²-2*k+1=(k-1)²=0. Оно имеет действительные и равные корни k1=k2=1, поэтому y1=C1*e^x+C2*x*e^x, где C1 и C2 - произвольные постоянные.
2) Займёмся отысканием y2. Так как числа m+i*n=3 и m-i*n=3 не являются корнями ХУ, то y2=e^(m*x)*[R1(x)*cos(n*x)+R2(x)*sin(n*x)]=e^(3*x)*R1(x), где R1(x) - многочлен, степень которого равна старшей из степеней многочленов P1(x) и P2(x). Так как эта старшая степень равна 0, то R1(x)=A, где A - неизвестная пока постоянная. Тогда y2=A*e^(3*x). Дважды дифференцируя y2, подставляя выражения для y2, y2' и y2" в уравнение и приводя подобные члены, приходим к уравнению: 4*A*e^(3*x)=8*e^(3*x). Решая его, находим A=2. Отсюда y2=2*e^(3*x).
3) Находим y(x)=C1*e^x+C2*x*e^x+2*e^(3*x). Дифференцируя y(x) и используя начальные условия, получаем систему уравнений:
C1+2=5
C1+C2+6=8
Решая её, находим C1=3, C2=-1. Отсюда искомое частное решение уравнения y=3*e^x-x*e^x+2*e^(3*x).
1) 223
2) Воды стало поровну
Пошаговое объяснение:
1) Сумма последовательных десяти чисел — это сумма членов арифметической прогрессии с разностью 1. Пусть первый член равен a. Тогда сумма a, a + 1, ... , a + 9 равна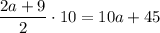
, а стёртый член равен 
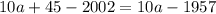. Стёртый член должен быть не меньше первого члена прогрессии и не больше последнего:
Рассмотрим десять последовательных чисел, начиная с 218 (218, 219, ... , 227). Их сумма равна 10 * 218 + 45 = 2225. Стёртый член равен 2225 - 2002 = 223. Он содержится в последовательности, так как 218 < 223 < 227. Значит, ответ верный.
2) В первом стакане количество воды увеличилось в 1,01 * 1,02 * ... * 1,27 раз. Во втором стакане количество воды увеличилось в 1,27 * 1,26 * ... * 1,01. Множители в этих произведениях равны, значит, оба произведения равны. Количество воды в обоих стаканах увеличилось в одинаковое количество раз.
ответ: y=3*e^x-x*e^x+2*e^(3*x).
Пошаговое объяснение:
Перед нами - линейное неоднородное ДУ 2 порядка с постоянными коэффициентами и с правой частью "специального" вида f(x)=e^(m*x)*[P1(x)*cos(n*x)+P2(x)*sin(n*x)], где m=3, n=0, P1(x)=8, P2(x)=0. Его решение y(x)=y1+y2, где y1 - общее решение однородного ДУ y"-2*y'+y=0, а y2 - частное решение данного неоднородного ДУ.
1) Найдём y1. Составляем характеристическое уравнение (ХУ): k²-2*k+1=(k-1)²=0. Оно имеет действительные и равные корни k1=k2=1, поэтому y1=C1*e^x+C2*x*e^x, где C1 и C2 - произвольные постоянные.
2) Займёмся отысканием y2. Так как числа m+i*n=3 и m-i*n=3 не являются корнями ХУ, то y2=e^(m*x)*[R1(x)*cos(n*x)+R2(x)*sin(n*x)]=e^(3*x)*R1(x), где R1(x) - многочлен, степень которого равна старшей из степеней многочленов P1(x) и P2(x). Так как эта старшая степень равна 0, то R1(x)=A, где A - неизвестная пока постоянная. Тогда y2=A*e^(3*x). Дважды дифференцируя y2, подставляя выражения для y2, y2' и y2" в уравнение и приводя подобные члены, приходим к уравнению: 4*A*e^(3*x)=8*e^(3*x). Решая его, находим A=2. Отсюда y2=2*e^(3*x).
3) Находим y(x)=C1*e^x+C2*x*e^x+2*e^(3*x). Дифференцируя y(x) и используя начальные условия, получаем систему уравнений:
C1+2=5
C1+C2+6=8
Решая её, находим C1=3, C2=-1. Отсюда искомое частное решение уравнения y=3*e^x-x*e^x+2*e^(3*x).