Угол, опирающийся на дугу имеет градусную меру в 2 раза меньше этой дуги.
Углы ABC и AOC опираются на одну дугу AC (правда, AOC - центральный угол, поэтому его градусная мера совпадает с длиной дуги, на которую он опирается). Значит угол AOC в 2 раза больше угла ABC = 126 градусов.
Углы AOB и OCB опираются (суммарно) на оставшуюся окружность и их суммарная градусная мера = 360 - 126 = 234 градуса.
Рассмотрим 2 треугольника AOB и BOC. Суммарная градусная мера их углов = 180 * 2 = 360.
Распишем эти углы: BAO + AOB + OBA + OCB + CBO + BOC.
Геометрическая прогрессия это умножение. q - коэффицент.
Есть формула
По данной формуле подставим наши значения
b(2) = -1,1*2 = -2,2
b(3) = -2,2*2=-4,4 (или b(3)=-1,1*2^2=-1,1*4=-4,4)
Если у нас известен первый член геометрической прогрессии и коэффиент и надо найти какой-нибудь член под номер 10, можно прост перемножать первый член на коэффицент, если забыл формулу (10 раз)
И так, надо найти сумму
b(1)=-1,1
b(2)=-2,2
b(3)=-4,4
S(3)=-1,1+(-2,2)+(-4,4)=-7,7 (+ перед скобкой не меняет знака, сл-но - остается)
Это один из в лоб, есть формула нахождения суммы членов геометрическй прогрессии
Попробуем найти по этой формуле, ( -1,1 (2^3-1) )/ (2-1) = -7,7
Формулой удобно, но если забыл, то только в лоб, или выводить формулу)
Угол, опирающийся на дугу имеет градусную меру в 2 раза меньше этой дуги.
Углы ABC и AOC опираются на одну дугу AC (правда, AOC - центральный угол, поэтому его градусная мера совпадает с длиной дуги, на которую он опирается). Значит угол AOC в 2 раза больше угла ABC = 126 градусов.
Углы AOB и OCB опираются (суммарно) на оставшуюся окружность и их суммарная градусная мера = 360 - 126 = 234 градуса.
Рассмотрим 2 треугольника AOB и BOC. Суммарная градусная мера их углов = 180 * 2 = 360.
Распишем эти углы: BAO + AOB + OBA + OCB + CBO + BOC.
BAO = 41 (по условию)
AOB + BOC = 234 (см. выше)
OBA + CBO = ABC = 63 (по условию)
Итого 41 + 234 + 63 + OCB = 360
338 + OCB = 360
OCB = 22
-7,7
Пошаговое объяснение:
Геометрическая прогрессия это умножение. q - коэффицент.
Есть формула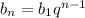
По данной формуле подставим наши значения
b(2) = -1,1*2 = -2,2
b(3) = -2,2*2=-4,4 (или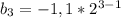
b(3)=-1,1*2^2=-1,1*4=-4,4)
Если у нас известен первый член геометрической прогрессии и коэффиент и надо найти какой-нибудь член под номер 10, можно прост перемножать первый член на коэффицент, если забыл формулу (10 раз)
И так, надо найти сумму
b(1)=-1,1
b(2)=-2,2
b(3)=-4,4
S(3)=-1,1+(-2,2)+(-4,4)=-7,7 (+ перед скобкой не меняет знака, сл-но - остается)
Это один из в лоб, есть формула нахождения суммы членов геометрическй прогрессии
Попробуем найти по этой формуле, ( -1,1 (2^3-1) )/ (2-1) = -7,7
Формулой удобно, но если забыл, то только в лоб, или выводить формулу)