На сбор приглашено 120 спортсменов. вероятность того, что выбранный случайным образом спортсмен выполнит нормативы комплекса гто первой ступени, равна 0,7. определить вероятность того, что не мене 60 спортсменов выполнят эти нормативы.

Показать ответ

Ответ:

Зеф3

11.12.2020 18:21

Можно сравнить их книги тремя книги только со сказками, только со стихами и книги вместе.
Первый сравниваем книги со стихами)
У Диляры их 14, у Сардара - 8.
14 > 8, следовательно, у Диляры больше книг со стихами, чем у Сардара.
Второй сравниваем книги со сказками)
У Диляры их 20, у Сардара - 30.
20 < 30, следовательно, у Сардара больше книг со сказками, чем у Диляры.
Третий сравниваем общее количество книг)
У Диляры их 34 (14 + 20=34), а у Сардара - 38 (8 + 30 =38)
34 < 38, следовательно, у Диляры меньше книг со стихами и сказками, чем у Сардара.

0,0(0 оценок)

Ответ:

ангелина67890

10.07.2021 04:32

Задача первая. Событие А состоит в том, что нужная формула содержится в первой книге

Событие В состоит в том, что нужная формула содержится во второй книге

Событие С состоит в том, что нужная формула содержится в третьей книге

а) Вероятность того, что формула содержится только в одной книге, равна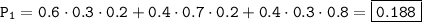 $\tt P_1=0.6\cdot0.3\cdot0.2+0.4\cdot0.7\cdot0.2+0.4\cdot0.3\cdot0.8=\boxed{\tt0.188}$

б) Вероятность того, что формулы содержатся в ни одной книге, равна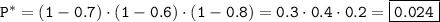 $\tt P^*=(1-0.7)\cdot(1-0.6)\cdot(1-0.8)=0.3\cdot0.4\cdot0.2=\boxed{\tt 0.024}$

в) Вероятность того, что формула содержится хотя бы в двух книгах, равна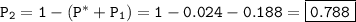 $\tt P_2=1-(P^*+P_1)=1-0.024-0.188=\boxed{\tt 0.788}$

Задача вторая.

Событие А - лампа является рабочей.

а) Найдем вероятность того, что лампа проработает заданное число часов по формуле полной вероятности

$\tt P(A)=P(A|H_1)P(H_1)+P(A|H_2)P(H_2)+P(A|H_3)P(H_3)=0.8\cdot0.6+0.7\cdot0.3+\\ +0.9\cdot0.1=0.78$

Вероятность того, что лампа не проработает заданное число часов, равна

$\tt \overline{\tt P(A)}=1-P(A)=1-0.78=\boxed{\tt0.22}$

б) Найдем вероятность того, что лампа, проработавшая заданное число часов, принадлежит первой партии по формуле Байеса:

$\displaystyle \tt P(H_1|A)=\frac{P(A|H_1)P(H_1)}{P(A)} =\frac{0.8\cdot0.6}{0.78} \approx \boxed{\tt 0.615}$

Задача третья. а) Найдем вероятность того, что что из десяти посеянных семян взойдут 8 семян по формуле Бернулли:

$\tt P_{10}\{k=8\}=C^8_{10}p^8(1-p)^2=\dfrac{10!}{2!8!} \cdot0.7^8\cdot0.3^2\approx\boxed{\tt0.23}$

б) Вероятность того, что из десяти посеянных семян взойдут по крайней мере 8 семян, равна:

$\tt P_{10}\{k\geq8\}=P_{10}\{k=8\}+P_{10}\{k=9\}+P_{10}\{k=10\}=\\ =C^8_{10}p^8(1-p)^2+C^9_{10}p^9(1-p)+p^{10}=\dfrac{10!}{2!8!} \cdot0.7^8\cdot0.3^2+\\ \\ +10\cdot0.7^9\cdot0.3+0.7^{10}\approx\boxed{\tt 0.383}$