Итак, наше число делится на 10(исходя из 3его предложения в условии), а значит и заканчивается на 0. Тогда оно имеет вид , откуда перевернутое частное выглядит как .
Так как цифры отличаются на 2, то все они одной четности. В нашем распоряжении осталось 4 четных(0 ведь уже был использован) и 5 нечетных. Очевидно, что наше 5и-значное число, состоящее из различных цифр(так как при делении на 10 числа, кратного 10, отбрасывается 0), либо 13579, либо 97531.
Значит искомое число 975310 или 135790
Учитывая, что было составлено наибольшее из возможных чисел, то число равно 975310
1) при аннуитетных платежах Остап платит каждый раз одну и ту же сумму x$. За 1 месяц банк начислил 20% и долг стал 3640*1,2=4368. Остап заплатил х. Долг стал 4368-x. За 2 месяц банк начислил 20% и долг стал (4368-x)*1,2 = 5241,6-1,2*x. Остап заплатил х и долг стал 5241,6-2,2x. За 3 месяц банк начислил 20% и долг стал (5241,6-2,2x)*1,2 = 6289,92-2,64x. Остап заплатил x и долг стал 0. 6289,92-3,64x = 0 x = 6289,92/3,64 = 1728 $ платит Остап каждый месяц. Всего он заплатит 1728*3 = 5184. 2) при дифференцированных платежах всё намного сложнее. Начальный долг был 3640. Банк начислил 20%, долг стал 4368. Остап заплатил y1, долг стал 4368-y1. При этом долг уменьшился на некоторую величину z. 4368-y1 = 3640-z z = y1 - 728 На 2 месяц банк начислил 20%, долг стал (4368-y1)*1,2 = 5241,6-1,2*y1. Остап заплатил y2, долг стал 5241,6-1,2*y1-y2. И он опять уменьшился на z. 5241,6-1,2*y1-y2 = 4368-y1-z y2 = 5241,6-4368-0,2*y1+z = 873,6-0,2*y1+y1-728 = 0,8*y1+145,6 Долг равен 5241,6-1,2*y1-y2 = 5241,6-1,2*y1-0,8*y1-145,6 = 5096-2*y1 На 3 месяц банк начислил 20%, долг стал (5096-2*y1)*1,2 = 6115,2-2,4*y1 Остап заплатил y3, и долг стал 6115,2-2,4*y1-y3. И опять он уменьшился на z. 6115,2-2,4*y1-y3 = 5096-2*y1-z y3 = 6115,2-5096-0,4*y1+y1-728 = 0,6*y1+291,2. Долг стал равен 6115,2-2,4*y1-0,6*y1-291,2 = 5824 - 3*y1. Но это последняя выплата, и долг стал равен 0. 5824 = 3*y1 y1 = 5824/3 = 1941,(3) = 1941 1/3 y2 = 0,8*y1+145,6 = 1698,(6) = 1698 2/3 y3 = 0,6*y1+291,2 = 1456. Долг уменьшался каждый раз на z = y1-728 = 1941 1/3 - 728 = 1213 1/3 Всего Остап заплатит y1+y2+y3 = 1941 1/3 + 1698 2/3 + 1456 = 5096. При втором плане платежей Остап сэкономит 5184-5096=88$. При объеме выплат больше 5000 такая копеечная экономия не стоит трудов по её вычислению.
Итак, наше число делится на 10(исходя из 3его предложения в условии), а значит и заканчивается на 0. Тогда оно имеет вид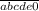
, откуда перевернутое частное выглядит как 
.
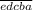Так как цифры отличаются на 2, то все они одной четности. В нашем распоряжении осталось 4 четных(0 ведь уже был использован) и 5 нечетных. Очевидно, что наше 5и-значное число, состоящее из различных цифр(так как при делении на 10 числа, кратного 10, отбрасывается 0), либо 13579, либо 97531.
Значит искомое число 975310 или 135790
Учитывая, что было составлено наибольшее из возможных чисел, то число равно 975310
За 1 месяц банк начислил 20% и долг стал 3640*1,2=4368.
Остап заплатил х. Долг стал 4368-x.
За 2 месяц банк начислил 20% и долг стал
(4368-x)*1,2 = 5241,6-1,2*x.
Остап заплатил х и долг стал 5241,6-2,2x.
За 3 месяц банк начислил 20% и долг стал
(5241,6-2,2x)*1,2 = 6289,92-2,64x.
Остап заплатил x и долг стал 0.
6289,92-3,64x = 0
x = 6289,92/3,64 = 1728 $ платит Остап каждый месяц.
Всего он заплатит 1728*3 = 5184.
2) при дифференцированных платежах всё намного сложнее.
Начальный долг был 3640.
Банк начислил 20%, долг стал 4368. Остап заплатил y1, долг стал 4368-y1.
При этом долг уменьшился на некоторую величину z.
4368-y1 = 3640-z
z = y1 - 728
На 2 месяц банк начислил 20%, долг стал
(4368-y1)*1,2 = 5241,6-1,2*y1.
Остап заплатил y2, долг стал
5241,6-1,2*y1-y2.
И он опять уменьшился на z.
5241,6-1,2*y1-y2 = 4368-y1-z
y2 = 5241,6-4368-0,2*y1+z = 873,6-0,2*y1+y1-728 = 0,8*y1+145,6
Долг равен 5241,6-1,2*y1-y2 = 5241,6-1,2*y1-0,8*y1-145,6 = 5096-2*y1
На 3 месяц банк начислил 20%, долг стал
(5096-2*y1)*1,2 = 6115,2-2,4*y1
Остап заплатил y3, и долг стал 6115,2-2,4*y1-y3.
И опять он уменьшился на z.
6115,2-2,4*y1-y3 = 5096-2*y1-z
y3 = 6115,2-5096-0,4*y1+y1-728 = 0,6*y1+291,2.
Долг стал равен
6115,2-2,4*y1-0,6*y1-291,2 = 5824 - 3*y1.
Но это последняя выплата, и долг стал равен 0.
5824 = 3*y1
y1 = 5824/3 = 1941,(3) = 1941 1/3
y2 = 0,8*y1+145,6 = 1698,(6) = 1698 2/3
y3 = 0,6*y1+291,2 = 1456.
Долг уменьшался каждый раз на
z = y1-728 = 1941 1/3 - 728 = 1213 1/3
Всего Остап заплатит
y1+y2+y3 = 1941 1/3 + 1698 2/3 + 1456 = 5096.
При втором плане платежей Остап сэкономит 5184-5096=88$.
При объеме выплат больше 5000 такая копеечная экономия не стоит трудов по её вычислению.