На стороне ав параллелограмма abcd отмечена произвольная точка g. докажите, что сумма площадей треугольников acg и bdg равна половине площади данного параллелограмма
2) Для двузначных она дает для числа (a обозначает первую цифру, b - вторую)
То есть мы берем первую цифру нашего двузначного числа и умножаем ее на 9. Например 38 -> 27.
Из этих двух свойств понятно, что непосредственно перед нулем шло однозначное число, причем кратное 9. То есть это и было 9. До этого шли двузначные числа, но они все были результатом этой операции, а потому должны быть кратны 9. Таким образом, очень легко восстанавливаем конец этой последовательности:
0 9 18 27 36 45 54 63 72 81
(в обратном порядке)
Следующее число должно быть либо 90, либо 99. Ясно что оно получалось из трехзначного числа. Но первые десять трехзначных чисел дают 99, а следующие уже слишком большие. Из этого заключаем, что последовательность заканчивается так:
99 и любое число от 100 до 109.
Таким образом ответ на вопрос: любое от 100 до 109.
120 не делится на 9, а на 8 делится, 120:8=15 - не подходит, т.к. получится 4 цифры в числе и которое делится только на нечётные числа - 5 и 3. Значит, вторая 8 не подходит. На 7 также не делится, а на число 6 делится, получаем 20, которое делится на 5, 2, 2
Возьмём 2*3 = 6, будет наибольшим из оставшихся вариантов:
любое от 100 до 109
Пошаговое объяснение:
Изучим операцию вычитания суммы цифр из числа.
1) Для однозначных чисел она дает 0.
2) Для двузначных она дает для числа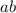
(a обозначает первую цифру, b - вторую)
То есть мы берем первую цифру нашего двузначного числа и умножаем ее на 9. Например 38 -> 27.
Из этих двух свойств понятно, что непосредственно перед нулем шло однозначное число, причем кратное 9. То есть это и было 9. До этого шли двузначные числа, но они все были результатом этой операции, а потому должны быть кратны 9. Таким образом, очень легко восстанавливаем конец этой последовательности:
0 9 18 27 36 45 54 63 72 81
(в обратном порядке)
Следующее число должно быть либо 90, либо 99. Ясно что оно получалось из трехзначного числа. Но первые десять трехзначных чисел дают 99, а следующие уже слишком большие. Из этого заключаем, что последовательность заканчивается так:
99 и любое число от 100 до 109.
Таким образом ответ на вопрос: любое от 100 до 109.
86 522 - пятизначное число, у которого произведение цифр равно 960, а последняя цифра - чётная
Пошаговое объяснение:
Разложим данное данное число на множители:
960 = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 5
Далее, из полученных множителей соберём 5 цифр:
9 - наибольшее число - не подходит, 960 не делится на 9 нацело. Возьмём 8: 960 : 8 = 120;
Разложим число 8 на множители: 8 = 2 * 2 * 2
960 = 2 * 2 * 2 * 2 * 2 * 2 * 3 * 5 ⇒ 8 * 2 * 2 * 2 * 3 * 5
120 не делится на 9, а на 8 делится, 120:8=15 - не подходит, т.к. получится 4 цифры в числе и которое делится только на нечётные числа - 5 и 3. Значит, вторая 8 не подходит. На 7 также не делится, а на число 6 делится, получаем 20, которое делится на 5, 2, 2
Возьмём 2*3 = 6, будет наибольшим из оставшихся вариантов:
8 * 2 * 2 * 2 * 3 * 5 ⇒ 8 * 2 * 2 * 6 * 5 - пять цифр наибольшего числа
86 522 - число, произведение цифр которого равно 960 и последняя цифра - чётная :
8 * 6 * 5 * 2 * 2 = 960.