Это оригинальная задача перенесем cos^2 2x вправую сторону имеем 1-cos^2 2x+tg^4 x=0 по осн триг тождеству имеем sin^2 2x+tg^4 x=0 тк квадраты всегда не отрицательны то sin^2 2x>=0 и tg^4 x>=0 то есть их сумма равна нулю только когда они оба равны нулю то есть уравнение равносильно системе sin2x=0 и tgx=0 если tgx=0 то и sinx=0 sin2x=2*cosx*sinx=0 то есть первое уравнение следует из второго тогда осталось решить tgx=0 x=pi*n n-целое то есть решения из промежутка -2pi -pi o pi 2pi то есть всего 5 решений ответ:5
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a. После первой выплаты сумма долга составит: S1 = Sb − X. После второй выплаты сумма долга составит: S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X. После третьей выплаты сумма оставшегося долга равна: S3 = Sb³ - (1-b+b²)X = Sb³ - · X После четвертой выплаты сумма оставшегося долга равна: S4 = - (1 + b +b² + b³)X = - · X По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому - · X = 0. Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается: X = рублей
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.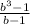 · X
· X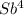 - (1 + b +b² + b³)X =
- (1 + b +b² + b³)X = 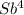 -
- 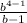 · X
· X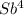 -
- 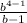 · X = 0.
· X = 0.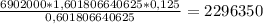 рублей
рублей
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -
После четвертой выплаты сумма оставшегося долга равна:
S4 =
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X =