Покажем, что при любых натуральных m и n числа 3m+5n+1 и 5m+9n+2 имеют разную чётность. Для этого вычтем из одного другое.
5m+9n+2-3m-5n-1=2m+4n+1=2(m+2n)+1 - нечётное число. Но как известно разность чисел одинаковой чётности - чётное число, а разной чётности - нечётное. Значит, числа 3m+5n+1 и 5m+9n+2 имеют разную чётность, то есть при любых m и n среди них будет одно чётное число. Но тогда в его разложении на простые множители содержится 2, которая при возведении в степень (6 или 7, в зависимости какое число оказалось чётным) даст множитель 64 или 128. Из чего следует, что число будет делиться на 64, то есть будет делиться на
Пошаговое объяснение:
Покажем, что при любых натуральных m и n числа 3m+5n+1 и 5m+9n+2 имеют разную чётность. Для этого вычтем из одного другое.
5m+9n+2-3m-5n-1=2m+4n+1=2(m+2n)+1 - нечётное число. Но как известно разность чисел одинаковой чётности - чётное число, а разной чётности - нечётное. Значит, числа 3m+5n+1 и 5m+9n+2 имеют разную чётность, то есть при любых m и n среди них будет одно чётное число. Но тогда в его разложении на простые множители содержится 2, которая при возведении в степень (6 или 7, в зависимости какое число оказалось чётным) даст множитель 64 или 128. Из чего следует, что число будет делиться на 64, то есть
будет делиться на 64, то есть  будет делиться на
будет делиться на 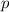
299.
х - высота треугольника
1,5х - основание
0,75х - половина основания
Тогда по теореме Пифагора:
х^2 + (0.75x)^2 = 50^2
1,5625x^2 = 2500
x^2 = 1600
x = 40 (см) - высота треугольника (х=-40 не удовлетвор.условиям задачи)
40*1,5=60 (см) - основание треугольника
60:2=30 (см) - средняя линия
S = 0,5ah = 0,5*60*40 = 1200 (кв см)
Найдём полупериметр
р = (50+50+60)/2 = 80 (см)
Воспользуемся формулами площади через радиусы вписанной и описанной окружности:
S = pr, r = S/p = 1200/80 = 15 (см)
S = abc/(4R), R = abc/(4S) = 50*50*60/(4*1200) = 31,25 (см)
300. ответ и решение во вложении