dx/dt=-6Asin6t+6Bcos6t и (d^2 x)/(dt^2 )=-36Acos6t-36Bsin6t
Выполняем подстановку: (d^2 x)/(dt^2 )+36x=0
-36(Acos6t+Bsin6t)+36x=0
-36x+36x=0
В результате получили тождество, а это означает, что функция x=Acos6t+Bsin6t является решением указанного дифференциального уравнения (d^2 x)/(dt^2 )+36x=0. Подставляем π/4 в x: Acos 3π/2+Bsin 3π/2=-2 и получаем B=2. Подставляем π/4 в dx/dt:-6Asin 3π/2+6Bcos 3π/2=12√3 и получаем A=2√3.
1) D = R. 2) D = (-∞; 5) U (5; +∞). 3) D = (-∞; -3) U (-3; 2) U (2; +∞). 4) D = (-∞;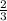 ) U (
) U ( 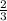 ; +∞). 5) D = (-∞; -3) U (-3; +∞).
; +∞). 5) D = (-∞; -3) U (-3; +∞).
Пошаговое объяснение:
Как мы знаем, D = множество аргументов, при котором уравнение имеет смысл.
1) y =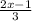 , и здесь будет D = R (любое число), т.к. делитель всегда будет 3.
, и здесь будет D = R (любое число), т.к. делитель всегда будет 3.
2) y =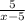 ,
,
х - 5 ≠ 0;
x ≠ 5.
D = (-∞; 5) U (5; +∞).
3) y =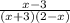 ,
,
1. х + 3 ≠ 0
2. х ≠ -3.
1. 2 - х ≠ 0.
- х ≠ -2.
х ≠ 2.
D = (-∞; -3) U (-3; 2) U (2; +∞).
4) Корень ликвидируется, т.к. есть степень.
2х-5х+2 ≠ 0.
-3х + 2 ≠ 0.
-3х ≠ -2.
3х ≠ 2.
х ≠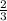 .
.
D = (-∞;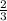 ) U (
) U ( 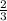 ; +∞).
; +∞).
5)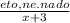 , х + 3 ≠ 0.
, х + 3 ≠ 0.
х ≠ -3.
D = (-∞; -3) U (-3; +∞).
Находим
dx/dt=-6Asin6t+6Bcos6t и (d^2 x)/(dt^2 )=-36Acos6t-36Bsin6t
Выполняем подстановку: (d^2 x)/(dt^2 )+36x=0
-36(Acos6t+Bsin6t)+36x=0
-36x+36x=0
В результате получили тождество, а это означает, что функция x=Acos6t+Bsin6t является решением указанного дифференциального уравнения (d^2 x)/(dt^2 )+36x=0. Подставляем π/4 в x: Acos 3π/2+Bsin 3π/2=-2 и получаем B=2. Подставляем π/4 в dx/dt:-6Asin 3π/2+6Bcos 3π/2=12√3 и получаем A=2√3.
ответ: x=2√3 cos6t+2sin6t частное решение.
Пошаговое объяснение: