Рассмотрим степени чисел 4, 5, 6, и 7, определим повторения в последних цифрах:
4¹=4, 4²=16=..6, 4³=64=..4, 4⁴=256=..6, Отсюда заключаем, что последняя цифра нечетных степеней числа 4 равен 4, тогда 4²⁰¹⁹=..4.
5¹=5, 5²=25=..5, 5³=125=..5, 5⁴=625=..5, Отсюда заключаем, что последняя цифра любых степеней числа 5 равен 5, тогда 5²⁰¹⁹=..5.
6¹=6, 6²=36=..6, 6³=216=..6, 6⁴=1296=..6, Отсюда заключаем, что последняя цифра любых степеней числа 6 равен 6, тогда 6²⁰¹⁹=..6.
7¹=7, 7²=49=..9, 7³=343=..3, 7⁴=2401=..1, 7⁵=7⁴⁺¹=..1·7¹=..7, ... Отсюда заключаем, что последние цифры степени числа 7 повторяются через каждые 4-степень, 7²⁰¹⁹=7²⁰¹⁶⁺³=..7³=..3.
2
Пошаговое объяснение:
4²⁰¹⁹ - 5²⁰¹⁹ + 6²⁰¹⁹ - 7²⁰¹⁹
Рассмотрим степени чисел 4, 5, 6, и 7, определим повторения в последних цифрах:
4¹=4, 4²=16=..6, 4³=64=..4, 4⁴=256=..6, Отсюда заключаем, что последняя цифра нечетных степеней числа 4 равен 4, тогда 4²⁰¹⁹=..4.
5¹=5, 5²=25=..5, 5³=125=..5, 5⁴=625=..5, Отсюда заключаем, что последняя цифра любых степеней числа 5 равен 5, тогда 5²⁰¹⁹=..5.
6¹=6, 6²=36=..6, 6³=216=..6, 6⁴=1296=..6, Отсюда заключаем, что последняя цифра любых степеней числа 6 равен 6, тогда 6²⁰¹⁹=..6.
7¹=7, 7²=49=..9, 7³=343=..3, 7⁴=2401=..1, 7⁵=7⁴⁺¹=..1·7¹=..7, ... Отсюда заключаем, что последние цифры степени числа 7 повторяются через каждые 4-степень, 7²⁰¹⁹=7²⁰¹⁶⁺³=..7³=..3.
Тогда
4²⁰¹⁹ - 5²⁰¹⁹ + 6²⁰¹⁹ - 7²⁰¹⁹=..4 - ..5 + ..6 - ..3=..0 - ..8= ..2
ответ: 2
Пошаговое объяснение:
1) Получим уравнения трех прямых треугольника по формуле для прямой, проходящей через две точки:
Первая пара точек A,B:
Приведем уравнение к виду:
Вторая пара точек А,С:
⇒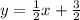
Третья пара точек B,C:
---
Теперь найдем тангенсы углов по формуле:
tgA - угол между прямыми AB и AC (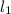 и
и 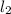 ):
):
tgB - угол между прямыми AB и BC (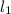 и
и 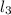 ):
):
tgC - угол между прямыми AC и BC (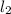 и
и 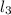 ):
):
Здесь 0 в знаменателе означает, что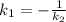 , а это условие перпендикулярности прямых. То есть угол C равен 90°.
, а это условие перпендикулярности прямых. То есть угол C равен 90°.