При переливании воды из одного сосуда в другой, объем воды, естественно, не меняется. Пусть r - радиус основания первого сосуда. Тогда площадь основания: S=πr2 Объем воды: V=S*h=πr2h Площадь основания второго сосуда: S2=πR2=π(2r)2=4πr2 (R - радиус второго сосуда = 2r, по условию) Объем воды: V2=S2*h2=4πr2h2 Как мы уже сказали ранее объем воды не меняется, т.е. V=V2, получаем: πr2h=4πr2h2 |:πr2 h=4h2 80=4h2 h2=80/4=20 ответ: 20 Поделитесь решением Присоединяйтесь к нам... Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас' Другие задачи из этого раздела Задача №E3004A В трапеции ABCD известно, что AD=8, BC=7, а её площадь равна 45. Найдите площадь треугольника ABC. Задача №F4E4F0 В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров. Задача №F8A540 В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. ответ дайте в градусах. Задача №868E4C План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. ответ дайте в квадратных метрах. Задача №C1234A В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √34. Найдите объём параллелепипеда ABCDA1B1C1D1.
При переливании воды из одного сосуда в другой, объем воды, естественно, не меняется. Пусть r - радиус основания первого сосуда. Тогда площадь основания: S=πr2 Объем воды: V=S*h=πr2h Площадь основания второго сосуда: S2=πR2=π(2r)2=4πr2 (R - радиус второго сосуда = 2r, по условию) Объем воды: V2=S2*h2=4πr2h2 Как мы уже сказали ранее объем воды не меняется, т.е. V=V2, получаем: πr2h=4πr2h2 |:πr2 h=4h2 80=4h2 h2=80/4=20 ответ: 20 Поделитесь решением Присоединяйтесь к нам... Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас' Другие задачи из этого раздела Задача №E3004A В трапеции ABCD известно, что AD=8, BC=7, а её площадь равна 45. Найдите площадь треугольника ABC. Задача №F4E4F0 В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,8 раза. Найдите объём детали. ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров. Задача №F8A540 В трапеции ABCD известно, что AB=CD, ∠BDA=54° и ∠BDC=23°. Найдите угол ABD. ответ дайте в градусах. Задача №868E4C План местности разбит на клетки. Каждая клетка обозначает квадрат 1м х 1м. Найдите площадь участка, выделенного на плане. ответ дайте в квадратных метрах. Задача №C1234A В прямоугольном параллелепипеде ABCDA1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √34. Найдите объём параллелепипеда ABCDA1B1C1D1.
Пошаговое объяснение:
1) длина стороны квадрата 28 м
2) длина радиуса полукругов = 14 м
3) длина декоративного забора 9408 м
Пошаговое объяснение:
клумба получается примерно как на рисунке
здесь видно, что площадь клумбы S = S₁ + 4S₂
где S₁ - площадь квадрата S₂ - площадь полукруга
при этом сторона квадрата = диаметру круга = 2*радиус круга
пусть а - сторона квадрата, тогда d = a, r=1/2 a
теперь формулы
S₁ (площадь квадрата) = а²
S₂ (площадь круга) =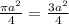
L (длина окружности) =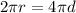
для площади круга нам нужно площадь квадрата + 4 площади полукруга или 2 площади круга, получим
1960 = S₁ + 2 S₂ = a² + 2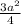
решаем относительно а и получим а=28 (м)
теперь считаем длину забора
L = 4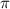 d² = 4*3*28² = 4*3* 784 = 9408 (м)
d² = 4*3*28² = 4*3* 784 = 9408 (м)
1) длина стороны квадрата 28 м
2) длина радиуса полукругов = 14 м
3) длина декоративного забора 9408 м