Пошаговое объяснение:
z=F(x0)-f ′ (x0)*(x-x0)
f ′(x)=cos(x)
f ′(x0)=f ′(П/6)=cos(П/6)=
f(x0)= f(П/6)=sin(П/6)=1/2
z=1/2 - *(П/6 - x)= 1/2- - = -=
ответ:z= - уравнение касательной в точке П/6
Пошаговое объяснение:
z=F(x0)-f ′ (x0)*(x-x0)
f ′(x)=cos(x)
f ′(x0)=f ′(П/6)=cos(П/6)=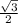
f(x0)= f(П/6)=sin(П/6)=1/2
z=1/2 -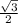
*(П/6 - x)= 1/2- 
-
= 
-
= 
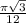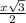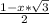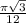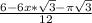
ответ:z=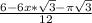
- уравнение касательной в точке П/6