Написать уравнение прямой L1, проходящей через точку M0(1;1) перпендикулярно к заданной прямой L: 2x-y-2=0

Показать ответ

Ответ:

Mikutyan01

04.03.2022 05:49

Пошаговое объяснение:

Пусть z км проплыли туристы по течению реки, тогда против течения они проплыли (19−z) км.

7−1=6 км/ч — скорость лодки против течения реки,

7+1=8 км/ч — скорость лодки по течения реки.

Чтобы найти время, надо расстояние делить на скорость, поэтому:

19−z6 ч — время, затраченное туристами на путь против течения реки, а

z8ч — время, затраченное туристами на путь по течения реки.

Зная, что в пути туристы были менее трёх часов, составим неравенство:

19−z6+z8<3

Чтобы избавиться от дроби, умножим обе части неравенства на 48.

(19−z6+z8)⋅48<3⋅4819−z6⋅48+z8⋅48<1448⋅(19−z)+6⋅z<144152−8z+6z<144−2z<−8:(−2)z>4

ответ: 4<z<19 км.

0,0(0 оценок)

Ответ:

УрсаПинкиПай

26.06.2022 05:14

В классе всего 12 + 18 = 30.

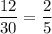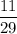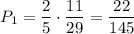
1) Вероятность выбрать первого мальчика равна $\dfrac{12}{30}=\dfrac{2}{5}$ . Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна $\dfrac{11}{29}$ . По теореме умножения, искомая вероятность: $P_1=\dfrac{2}{5}\cdot\dfrac{11}{29}=\dfrac{22}{145}$

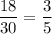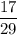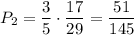
2) Выбрать первую девочку можно с вероятностью $\dfrac{18}{30}=\dfrac{3}{5}$ . В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна $\dfrac{17}{29}$ . По теореме умножения, искомая вероятность: $P_2=\dfrac{3}{5}\cdot\dfrac{17}{29}=\dfrac{51}{145}$

3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна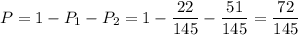 $P=1-P_1-P_2=1-\dfrac{22}{145}-\dfrac{51}{145}=\dfrac{72}{145}$