Пусть и задана в неявном виде
Тогда если , то
Следовательно,
Найдем
Находим уравнение касательной:
и уравнение нормали в этой же точке:
Пусть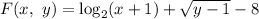 и задана в неявном виде
и задана в неявном виде 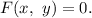
Тогда если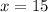 , то
, то
Следовательно,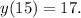
Найдем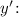
Находим уравнение касательной:
и уравнение нормали в этой же точке: