y = 2x + 2
Пошаговое объяснение:
Мы знаем, что уравнение касательной в точке представимо в виде
Подставим:
f(x) = 6x - 2x²; x₀ = -1
уравнение касательной
y = f'(-1) (x-(-1)) +f(-1)
f(-1) = -6 -2 = -8
f'(x) = 6-4x; f'(-1) = 10
уравнение касательной в точке х₀=(-1) имеет вид
у = 10х +2
y = 2x + 2
Пошаговое объяснение:
Мы знаем, что уравнение касательной в точке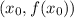 представимо в виде
представимо в виде 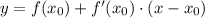
Подставим: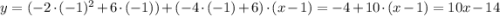
Пошаговое объяснение:
f(x) = 6x - 2x²; x₀ = -1
уравнение касательной
y = f'(-1) (x-(-1)) +f(-1)
f(-1) = -6 -2 = -8
f'(x) = 6-4x; f'(-1) = 10
уравнение касательной в точке х₀=(-1) имеет вид
у = 10х +2