Напишите уравнение касательной к графику функции - вопрос №220213396017 от ЛюБИмИЦа55 26.06.2021 13:07

Question

Математика: Напишите уравнение касательной к графику функции f(x)= x^2-2x в точке x0=2

ЛюБИмИЦа55 · Answer

Пошаговое объяснение:Ур-е касательной в общем виде:, тогда Находим производную y :Итого считаем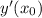 :Подставляем в общее уравнение все найденное:...