8. объем призмы равен произведению площади основания s=а²√3/4, где а- сторона правильного треугольника, на высоту, т.к. дан объем и высота, можно найти площадь основания призмы. она равна
3509√3/(4*29)=а²√3/4,⇒ 3509/29=а²; а²=121=11²⇒а=11см, высота основания призмы равна а√3/2, а радиус вписанной окружности r=(1/3)*а√3/2=(1/3)*11√3/2=11√3/6/см/,
1. т.к. площадь основания цилиндра равна πr²=121π⇒r²=11²⇒r=11cм, зная радиус, найдем диаметр основания. он равен 2*11=22/см/, по диаметру и высоте найдем диагональ осевого сечения, являющегося прямоугольником, у которого диагональ - гипотенуза прямоугольного треугольника с катетами, равными высоте и диаметру основания. По теореме Пифагора найдем диагональ осевого сечения цилиндра. Она равна √(13²+22²)=√(169+484)=√653/см/
А. 5 т продукции вида I, 6 т продукции вида II; прибыль — 400000 рублей
Б. I : II = 5 : 2
Пошаговое объяснение:
А. Пусть выпускается x тонн продукции вида I и y тонн продукции вида II. Тогда прибыль составит S(x, y) = 2x + 5y (в десятках тысяч рублей). Данную величину необходимо максимизировать. На x и y накладываются ограничения из-за времени работы станков: первый используется y часов, второй — x + 4y часов, третий — x + y часов. Тогда получаем
Изобразим данную область на графике. Искомой областью будет пересечение областей в I четверти (в силу неотрицательности x, y). Очевидно, функция S(x, y) максимальна, если x, y лежат на границе данной области (необходимое условие, так как, взяв любую другую точку, мы уменьшим x или y, тем самым уменьшим значение S). Найдём граничные точки, составляя и решая системы уравнений, соответствующие неравенствам системы. Получим A(0; 7), B(1; 7), C(5; 6), D(11; 0).
Если точка лежит на прямой y = 7, то S(x, 7) = 2x + 35 — возрастающая функция, максимум достигается в точке B, S(1, 7) = 37.
Если точка лежит на прямой , то — также возрастающая функция, максимум достигается в точке C, S(5, 6) = 40.
Если точка лежит на прямой y = 11 - x, то S(x, 11-x) = -3x + 55 — убывающая функция.
Таким образом, максимум достигается при x = 5, y = 6, прибыль составит 400000 рублей.
Б. Например, план придётся поменять, если чистые прибыли соотносятся как 5 : 2. Тогда S(x, y) = 5x + 2y. При прежнем плане S(5, 6) = 37, а уже при x = 11, y = 0 S(11, 0) = 55 > 37.
8. объем призмы равен произведению площади основания s=а²√3/4, где а- сторона правильного треугольника, на высоту, т.к. дан объем и высота, можно найти площадь основания призмы. она равна
3509√3/(4*29)=а²√3/4,⇒ 3509/29=а²; а²=121=11²⇒а=11см, высота основания призмы равна а√3/2, а радиус вписанной окружности r=(1/3)*а√3/2=(1/3)*11√3/2=11√3/6/см/,
1. т.к. площадь основания цилиндра равна πr²=121π⇒r²=11²⇒r=11cм, зная радиус, найдем диаметр основания. он равен 2*11=22/см/, по диаметру и высоте найдем диагональ осевого сечения, являющегося прямоугольником, у которого диагональ - гипотенуза прямоугольного треугольника с катетами, равными высоте и диаметру основания. По теореме Пифагора найдем диагональ осевого сечения цилиндра. Она равна √(13²+22²)=√(169+484)=√653/см/
А. 5 т продукции вида I, 6 т продукции вида II; прибыль — 400000 рублей
Б. I : II = 5 : 2
Пошаговое объяснение:
А. Пусть выпускается x тонн продукции вида I и y тонн продукции вида II. Тогда прибыль составит S(x, y) = 2x + 5y (в десятках тысяч рублей). Данную величину необходимо максимизировать. На x и y накладываются ограничения из-за времени работы станков: первый используется y часов, второй — x + 4y часов, третий — x + y часов. Тогда получаем
Изобразим данную область на графике. Искомой областью будет пересечение областей в I четверти (в силу неотрицательности x, y). Очевидно, функция S(x, y) максимальна, если x, y лежат на границе данной области (необходимое условие, так как, взяв любую другую точку, мы уменьшим x или y, тем самым уменьшим значение S). Найдём граничные точки, составляя и решая системы уравнений, соответствующие неравенствам системы. Получим A(0; 7), B(1; 7), C(5; 6), D(11; 0).
Если точка лежит на прямой y = 7, то S(x, 7) = 2x + 35 — возрастающая функция, максимум достигается в точке B, S(1, 7) = 37.
Если точка лежит на прямой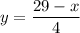
, то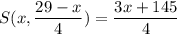 
— также возрастающая функция, максимум достигается в точке C, S(5, 6) = 40.
Если точка лежит на прямой y = 11 - x, то S(x, 11-x) = -3x + 55 — убывающая функция.
Таким образом, максимум достигается при x = 5, y = 6, прибыль составит 400000 рублей.
Б. Например, план придётся поменять, если чистые прибыли соотносятся как 5 : 2. Тогда S(x, y) = 5x + 2y. При прежнем плане S(5, 6) = 37, а уже при x = 11, y = 0 S(11, 0) = 55 > 37.