Рассмотрим полуокружность, расположенную в верхней полуплоскости. Для нее выразим у:
Необходимо найти касательную к графику функции , проходящую через точку .
Пусть - точка касания. Уравнение касательной:
Найдем производную:
Подставим все величины в уравнение касательной:
Поскольку касательная проходит через точку , то подставим координаты этой точки в уравнение:
Значит, уравнение касательной имеет вид:
Полуокружность , расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:
Таким образом, две касательные задаются уравнением:
Рассмотрим полуокружность, расположенную в верхней полуплоскости. Для нее выразим у:
Необходимо найти касательную к графику функции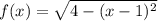 , проходящую через точку
, проходящую через точку 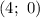 .
.
Пусть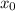 - точка касания. Уравнение касательной:
- точка касания. Уравнение касательной:
Найдем производную:
Подставим все величины в уравнение касательной:
Поскольку касательная проходит через точку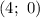 , то подставим координаты этой точки в уравнение:
, то подставим координаты этой точки в уравнение:
Значит, уравнение касательной имеет вид:
Полуокружность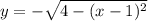 , расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:
, расположенная в нижней полуплоскости, симметрична относительно рассмотренной относительно оси абсцисс. Значит и касательная к ней будет симметрична:
Таким образом, две касательные задаются уравнением: