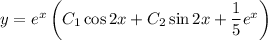№ 212.2 литра это два кубических дециметра. В одном дециметре 10 см, в 1-ом куб. дециметре 1000 см кубических. В 1 метре кубическом миллион см кубических. Нужно знать плотность керосина, это вроде 700 кг на метр кубический. 2000 см куб=0,002 метр куб. 0,002 умножить на 700 =1,4 кг.
№ 213.металлический кусок имеет объём 200 см кубических и массу 540 граммов. из какого металла этот кусок? какова его плотность?
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является .
1) — общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену где — некоторая постоянная. Тогда
Получили характеристическое уравнение:
Разделим обе части уравнения на :
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда
Воспользуемся формулой Эйлера:
Фундаментальная система решений: — функции линейно независимые, поскольку
Общее решение:
2) — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции .
Здесь , причем , поэтому частное решение имеет вид , где — неизвестный коэффициент, который нужно найти.
Тогда и подставим в исходное ЛНДР и найдем :
Разделим обе части уравнения на
Таким образом, частное решение:
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
№ 213.металлический кусок имеет объём 200 см кубических и массу 540 граммов. из какого металла этот кусок? какова его плотность?
№218.1,4*1*10^-3 и все это на плотность железа
№219.p = m/VОтсюдаV = m/p = 4 / 800 = 0.005 м³ - такой ёмкости нужна бутыль
№220.надо плотность нефти поделить на массу
№223.Если брать в среднем, 1 куб.метр песка весит 1,5 тонн.Значит в одном вагоне помещается 10 куб.метров песка.А для 400 000 куб.метров нужно 40 000 вагонов :
400 000 : 10 = 40 000
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является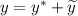 .
.
1)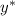 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену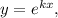 где
где 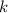 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 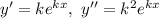
Получили характеристическое уравнение:
Разделим обе части уравнения на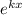 :
:
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда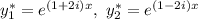
Воспользуемся формулой Эйлера: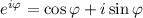
Фундаментальная система решений: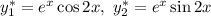 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 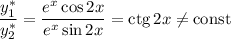
Общее решение: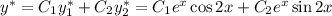
2)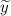 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 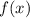 .
.
Здесь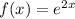 , причем
, причем 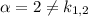 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 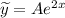 , где
, где 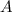 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда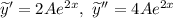 и
и 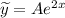 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 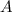 :
:
Разделим обе части уравнения на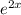
Таким образом, частное решение: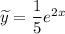
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
ответ: