Возьмем производную данной функции, чтобы затем найти экстремум:
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
Ну я попробую..
• По Пифагоровой тройке (признак прямоугольного треугольника), исходный ΔMKN - прямоугольный (сумма квадратов катетов, равна гипотенузе в квадрате)
• По теореме Пифагора:
MN² = MK² + KN²
8² + 15² = 17²
⇒ MN = 17
• Видим, что отрезок KF - медиана, а по свойству медианы прямоугольного треугольника:
KF = 1/2 MN = 1/2 * 17 = 8,5
• Ну и высота..
По метрическим соотношениям в прямоугольном Δ-ке:
KM² = ME * MN,
⇒ ME = KM²/MN
ME = 64/17 ≈ 3,76
• Отрезок EN = MN - ME = 17 - 3,76 = 13,24
• Рассмотрим ΔKEN - он прямоугольный (так как KE - высота), по теореме Пифагора:
KN² = KE² + EN²,
⇒ KE = √(KN² - EN²) = √(225 - 175,2976) = √49,7024 ≈ 7
ответ: Максимум - (4;29), Минимум - (0;-3)
Пошаговое объяснение:
(Как я понимаю, ночью ставки выше)
Возьмем производную данной функции, чтобы затем найти экстремум:
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
Значит:
При x = 0 -
При x = 4 -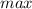
Подставим числа: