Математика: Найдите чему равна cosθ, sinθ, cos2θ

Найдите чему равна cosθ, sinθ, cos2θ

Показать ответ

Ответ:

lera5252

20.02.2022 09:14

c = 2a+b

Пошаговое объяснение:

Базис. Векторы a и b образуют базис, поскольку на плоскости (у векторов по две координаты) любые два линейно независимых вектора образуют базис (поскольку пространство двумерно), а линейная независимость на плоскости эквивалентна условию, что векторы непараллельны, т.е. их координаты непропорциональны. Впрочем, можно подойти и формально, записав линейную комбинацию векторов a и b, а также приравняв её к нулю:

$\alpha a+\beta b=0$

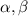$\left[\begin{array}{cc}3&1\\5&-7\end{array}\right] * \left[\begin{array}{c}\alpha \\\beta \end{array}\right] = \left[\begin{array}{c}0\\0 \end{array}\right]$

где $\alpha , \beta$ - числа. В силу того, что определитель матрицы векторов не равен нулю (матрица невырожденная), существует только нулевое решение, что означает линейную независимость векторов a и b.

Разложение. Чтобы найти разложение вектора c по базису, приравняем линейную комбинацию векторов a и b к вектору c:

$\alpha a+\beta b=c$

$\left[\begin{array}{cc}3&1\\5&-7\end{array}\right] * \left[\begin{array}{c}\alpha \\\beta \end{array}\right] = \left[\begin{array}{c}7\\3 \end{array}\right]$

Домножим левую и правую часть слева на обратную матрицу коэффициентов векторов:

$E*\left[\begin{array}{c}\alpha \\\beta \end{array}\right] =\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} * \left[\begin{array}{c}7\\3 \end{array}\right]$

Е - единичная матрица, можно опустить (получается при перемножении матрицы и обратной к ней).

$\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} = \left[\begin{array}{cc}\frac{7}{26} &\frac{1}{26} \\\frac{5}{26} &-\frac{3}{26} \end{array}\right]$ $\left[\begin{array}{cc}3&1\\5&-7\end{array}\right]^{-1} * \left[\begin{array}{c}7\\3 \end{array}\right] = \left[\begin{array}{cc}\frac{7}{26} &\frac{1}{26} \\\frac{5}{26} &-\frac{3}{26} \end{array}\right]* \left[\begin{array}{c}7\\3 \end{array}\right] = \left[\begin{array}{c}2\\1\end{array}\right] = \left[\begin{array}{c}\alpha \\\beta \end{array}\right]$

Итак,

$\alpha =2, \beta =1.$

Значит, c = 2a+b .

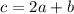Прямой проверкой можно убедиться в правильности ответа:

2a+b = 2*(3;5)+(1;-7) = (6;10)+(1;-7) = (7;3) = c.

0,0(0 оценок)

Ответ:

lizazarandiua

20.09.2021 14:40

Пошаговое объяснение:

1) цилиндр R=5cm h = 10 cm

если не дан угол наклона, считаем цилиндр прямым

Sполн = 2πRh + 2πR² = 2π(5*10 +25) = 150π (cm²)

V = πR²h = 250π (cm³)

2) конус R=9cm L = 15 cm

для начала найдем h

из сечения конуса, которым является равнобедренный треугольник со сторонами L =15 и основанием 18 найдем высоту треугольника. она и будет высотой конуса

h² = 15² -9² =144

h = 12cm

Sполн = πRL + πR² = π(9*15 +81) = 216π(cm²)

V = 1/3 (πR²h) = 324π(cm³)

Sсеч = Rh = 108 cm²

3) сфера S=π/4

радиус найдем из площади

S=4πR² ⇒ R = 1/4

V = 4/3 (πR³) = π/36 (cm³)

0,0(0 оценок)

Популярные вопросы: Математика