Первую половину пути Семён проехал на велосипеде, а вторую пешком. Он потратил на дорогу 1 час 45 минут. На обратном пути Семён весь путь пешком за 3 часа. За сколько времени (в минутах) он проехал бы обратный путь на велосипеде?
Формула движения: S=v*t
S - расстояние v - скорость t – время
Весь путь - 1;
0,5 - расстояние на велосипеде;
0,5 - расстояние пешком;
х - скорость на велосипеде;
у - скорость пешком;
0,5/х - время на велосипеде;
0,5/у - время пешком;
у * 3 - расстояние обратно пешком.
1 час 45 минут = 1 и 3/4 часа = 7/4 часа.
За сколько времени (в минутах) он проехал бы обратный путь на велосипеде?
По условию задачи система уравнений:
0,5/х + 0,5/у = 7/4
3у = 1
Преобразовать первое уравнение для упрощения, умножить все части уравнения на 4ху, чтобы избавиться от дробного выражения:
0,5 * 4у + 0,5 * 4х = 7ху
2х + 2у = 7ху
2х = 7ху - 2у
Выразить у во втором уравнении:
3у = 1
у = 1/3;
Подставить значение у в первое уравнение:
2х = 7х * 1/3 - 2 * 1/3
2х = 7х/3 - 2/3
Умножить все части уравнения на 3, чтобы избавиться от дробного выражения:
6х = 7х - 2
6х - 7х = -2
-х = -2
х = 2 (км/час) - скорость на велосипеде.
1 : 2 = 0,5 (часа) = 30 минут - за столько времени в минутах Семён проехал бы обратный путь на велосипеде.
Проверка:
Скорость на велосипеде в 6 раз больше скорости пешком:
В решении.
Пошаговое объяснение:
Первую половину пути Семён проехал на велосипеде, а вторую пешком. Он потратил на дорогу 1 час 45 минут. На обратном пути Семён весь путь пешком за 3 часа. За сколько времени (в минутах) он проехал бы обратный путь на велосипеде?
Формула движения: S=v*t
S - расстояние v - скорость t – время
Весь путь - 1;
0,5 - расстояние на велосипеде;
0,5 - расстояние пешком;
х - скорость на велосипеде;
у - скорость пешком;
0,5/х - время на велосипеде;
0,5/у - время пешком;
у * 3 - расстояние обратно пешком.
1 час 45 минут = 1 и 3/4 часа = 7/4 часа.
За сколько времени (в минутах) он проехал бы обратный путь на велосипеде?
По условию задачи система уравнений:
0,5/х + 0,5/у = 7/4
3у = 1
Преобразовать первое уравнение для упрощения, умножить все части уравнения на 4ху, чтобы избавиться от дробного выражения:
0,5 * 4у + 0,5 * 4х = 7ху
2х + 2у = 7ху
2х = 7ху - 2у
Выразить у во втором уравнении:
3у = 1
у = 1/3;
Подставить значение у в первое уравнение:
2х = 7х * 1/3 - 2 * 1/3
2х = 7х/3 - 2/3
Умножить все части уравнения на 3, чтобы избавиться от дробного выражения:
6х = 7х - 2
6х - 7х = -2
-х = -2
х = 2 (км/час) - скорость на велосипеде.
1 : 2 = 0,5 (часа) = 30 минут - за столько времени в минутах Семён проехал бы обратный путь на велосипеде.
Проверка:
Скорость на велосипеде в 6 раз больше скорости пешком:
2 (км/час) : 1/3 (км/час) = 6;
Времени на велосипеде потребуется в 6 раз меньше:
3 (часа) : 6 = 180 (минут) : 6 = 30 (минут), верно.
а)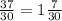
б)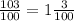
в)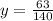
Пошаговое объяснение:
Привет! Давай решать.
А)
Переводим десятичную в обычную.
Получается такой пример:
Сейчас, нужно найти общий знаменатель:
В первой дроби знаменатель и числитель умножили на 5, во второй на 3.
Превращаем в целую, несократимую дробь.
Вот первая дробь решена.
Б)
Десятичную превращаем в обычную.
Приводим дроби к общему знаменателю:
В первой дроби знаменатель и числить умножаем на 5, а во второй ничего не умножаем. Вычисляем:
Превращаем в целую, несократимую дробь:
Вот вторая дробь решена.
В) Уравнение.
Приводим дроби к общему знаменателю:
Переносим дробь с левой части в правую через равно, меняя знак:
Вычисляем:
Вот уравнение и решено!