2) Воспользуемся формулой нахождения длины вектора: вектор |OP| (то есть серединная прямая АВ) = √x²+y²
Тогда решение: OP = √(-8²)+5² = 64+25 = 89
3) Воспользуемся формулой нахождения координат середины отрезка: x = ; y =
Тогда: x = ; y =
4) Строим центр окружности на координатных прямых, радиус окружности которой равняется 4. Нам нужно уравнение окружности. (Сорян, построишь сам всё, села батарея на телефоне)
Формула уравнения: (x - a)² + (y - b)² = r², а известные нам значения: a = 5, b = -6, r = 4
Часовая стрелка перемещается на 1 минутное деление за 12 минут. Одно минутное деление соответствует углу 6°.
В 4 часа 22 минуты часовая стрелка пройдет после 4 часового деления одно минутное и до второго ей не будет хватать 2 минут. То есть по угловой мере 1/6 от 6°, то есть 1°. (за 2 минуты часовая стрелка проходит 2/12 от минутного деления, то есть 1/6 или 1°) Так как минутная стрелка в этот момент будет указывать на второе минутное деление после 4 часов, то угол между часовой и минутной стрелкой в этот момент составит 1°
PS Oчевидно, что часовая и минутная стрелки должны почти совпадать. То есть угол между ними должен быть меньше, чем 6°. Это происходит в 1 час 5(6) минут, 2 часа 10(11) минут, 3 часа 16(17) минут и 4 часа 21(22) минуты, ну и так далее...)) Нам нужна разница между часовой и минутной в 2 минуты при условии, что минутная точно указывает на целое число минут. Так как за 2 минуты часовая проходит 1 градус. Поэтому в 4 часа 24 минуты часовая будет указывать точно на второе деление после 4 часов. А в 4 часа 22 минуты ей не будет хватать именно 2 минут до этого положения.
Ну и, в качестве примера, - почему нас не устроит время 0 часов 1 минута: 1 минута, которую минутная стрелка сместила ее на 6 градусов относительно часовой. В это же время часовая сместилась на 1/12 минутного деления от 12 часов, то есть на 0,5°. Промежуток между ними составил 6 - 0,5 = 5,5 градуса.
A (4;2) ; B (-8;5)
1) Воспользуемся формулой нахождения координат вектора: вектор AB = {x₂-x₁ ; y₂-y₁}
Для удобства сделаем так: A (x₁;y₁) B (x₂;y₂)
Тогда решение: {-8-4 ; 5-2} = {-12;3}
2) Воспользуемся формулой нахождения длины вектора: вектор |OP| (то есть серединная прямая АВ) = √x²+y²
Тогда решение: OP = √(-8²)+5² = 64+25 = 89
3) Воспользуемся формулой нахождения координат середины отрезка: x =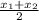 ; y =
; y = 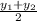
Тогда: x =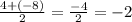 ; y =
; y = 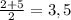
4) Строим центр окружности на координатных прямых, радиус окружности которой равняется 4. Нам нужно уравнение окружности. (Сорян, построишь сам всё, села батарея на телефоне)
Формула уравнения: (x - a)² + (y - b)² = r², а известные нам значения: a = 5, b = -6, r = 4
Вставляем в уравнение и решаем:
(x-5)² + (y+6)² = 16, распишем.
x²-10x+25 + y²+12y+36 = 16
x²-10x+25 + y²+12y+20 = 0
Решаем дискриминанты:
1) x²-10x+25 = 0
D = b²-4ac => (-10²)-4*1*25 = 100-100 = 0=0, 1 корень.
x =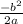
x₁ =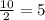
2) y²+12y+20 = 0
D = b²-4ac => 12²-4*1*20 = 144 - 80 = √64 = 8>0, 2 корня.
x =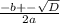
x₁ =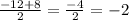
x₂ =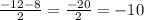
ответ: -10; -2; 5.
Часовая стрелка перемещается на 1 минутное деление за 12 минут.
Одно минутное деление соответствует углу 6°.
В 4 часа 22 минуты часовая стрелка пройдет после 4 часового
деления одно минутное и до второго ей не будет хватать 2 минут. То есть по угловой мере 1/6 от 6°, то есть 1°. (за 2 минуты часовая стрелка проходит 2/12 от минутного деления, то есть 1/6 или 1°)
Так как минутная стрелка в этот момент будет указывать на второе минутное деление после 4 часов, то угол между часовой и минутной стрелкой в этот момент составит 1°
PS Oчевидно, что часовая и минутная стрелки должны почти совпадать. То есть угол между ними должен быть меньше, чем 6°. Это происходит в 1 час 5(6) минут, 2 часа 10(11) минут, 3 часа 16(17) минут и 4 часа 21(22) минуты, ну и так далее...)) Нам нужна разница между часовой и минутной в 2 минуты при условии, что минутная точно указывает на целое число минут. Так как за 2 минуты часовая проходит 1 градус. Поэтому в 4 часа 24 минуты часовая будет указывать точно на второе деление после 4 часов. А в 4 часа 22 минуты ей не будет хватать именно 2 минут до этого положения.
Ну и, в качестве примера, - почему нас не устроит время 0 часов 1 минута:
1 минута, которую минутная стрелка сместила ее на 6 градусов относительно часовой. В это же время часовая сместилась на 1/12 минутного деления от 12 часов, то есть на 0,5°. Промежуток между ними составил 6 - 0,5 = 5,5 градуса.