Найдите количество решений уравнения x1+x2+x3+…+x9=41 в целых неотрицательных числах, при условии xi<=5 для всех i от 1 до 9.( Решения, отличающиеся друг от друга порядком следования чисел, считаются различными).
Далее заметим, что для любого верно . То есть верхнее ограничение выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Пошаговое объяснение:
Введем замену ;
;  .
.
Уравнение примет вид
Далее заметим, что для любого верно
верно  . То есть верхнее ограничение
. То есть верхнее ограничение  выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения 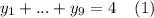 в целых неотрицательных числах.
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов