Поэтому любая комбинация векторов не выводит за пределы плоскости, уравнение которой легко найти, вычислив нормальный вектор как векторное произведение - здесь он весьма примитивен. Но для систематического подхода давайте проделаем общие выкладки: , , .
Смешанное произведение: , то есть векторы компланарны, что мы и заключили в самом начале.
Поэтому любая комбинация векторов не выводит за пределы плоскости, уравнение которой легко найти, вычислив нормальный вектор как векторное произведение![[\vec{BC},\;\vec{AC}] = \det\left(\begin{array}{ccc}\textbf{i}&\textbf{j}&\textbf{k}\\1&-2&0\\0&-1&0\end{array}\right)=(0,\;0,\;1)](/tpl/images/1614/2385/d613e.png) - здесь он весьма примитивен. Но для систематического подхода давайте проделаем общие выкладки:
- здесь он весьма примитивен. Но для систематического подхода давайте проделаем общие выкладки: 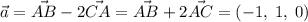 ,
, 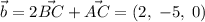 ,
, 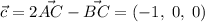 .
.
Смешанное произведение: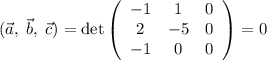 , то есть векторы компланарны, что мы и заключили в самом начале.
, то есть векторы компланарны, что мы и заключили в самом начале.