Найдите корень уравнения: 1) (1,8+x). 21 = 71,4;
7) 5,6 : (x - 6) = 8;
2) 16 (4x - 3,4)= 6,08;
8) 5,6 : x - 6 = 8;
3) (x - 1,25). 4,5 = 27;
9) 34,12 - x: 2,08 = 34,03;
4) (x +19,64). 0,18 = 144; 10) x: 100 - 1,2367 = 2,9633;
5) 17 (1,6 - 5x) = 2,38; 11) 9,2 (0,01y+0,412) = 4,6;
6) 9,66 : (x + 0,17) = 23; 12) 8,8 (0,12y - 0,04) = 0,44.
Пошаговое объяснение:
1) -59 - (-593) = -59 + 593 = 534 (минус на минус дает +, у 534 знак плюс, т.к. плюс у большего числа)
2) -(-526) - 431 = 526 - 431 = 95(минус на минус дает плюс).
3) -143 - (-142) = -143 + 142 = -1 (минус на минус дает плюс)
4) -(-325) + 69 = 325 + 69 = 394
5) -(-803) - 726 = 803 - 726 = 87
6) -(-643) - 54 = 643 - 54 = 589
7) -469 - 529 = -998 (а вот тут знак минус, т.к. он общий, то есть, у каждого числа)
8) -(-247) + 705 = 247 + 705 = 952
9) 69,276 - 843 = - 783,724
10) -(403) + 356 = -403 + 356 = -47
11) 831 + (-900) = -29
12) 1370 - (-1660) = 1370 + 1660 = 3030.
Выводы: 1) плюс на плюс дает плюс, минус на минус дает плюс, плюс на минус дает минус, минус на плюс дает минус.
2) Если у большего числа знак минус, то и у результата знак минус.
3) Если у большего числа знак плюс, то у результата будет плюс.
4) Если у обоих чисел знак минус, то у результата будет знак минус.
5) Если у обоих чисел знак плюс, то у результата будет плюс.
Задача решена.
1) зачеркнули 7 из числа 17;
2) зачеркнули 8 из числа 85.
Решение 1:Искомое двузначное число представим в виде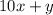
(
и 
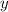- однозначные и неотрицательные, при этом 
).
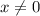1). Пусть зачеркнули цифру из разряда десятков. Тогда из числа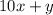
получилось число 
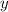. Нам нужно выполнение следующего равенства:
Единственные однозначные натуральные решения: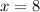
и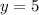 
.
Значит, число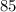
⇒ 
.
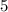2). Пусть зачеркнули цифру из разряда единиц.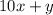
⇒ 
. Уравнение составляется и решается по аналогии:
Откуда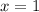
и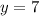 
.
Имеем второе подходящее решение: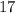
⇒ 
.
Значит, двузначное число - это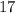 или
, или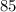 
.
Решение 2:Можно было и кратким подбором решить, умножая все цифры на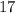
(умножаемая цифра - та, которая могла остаться после вычеркивания), пока не станут появляться трехзначные числа.
Нам нужно, чтобы в получившемся числе присутствовало умножаемое число (иначе как оно смогло бы потом остаться?):
Получаем те же самые два решения: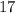
и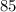 
.
Задача решена!