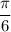Найдите корни уравнения 2 sin2 (3π / 2 – x) + 5 sin - вопрос №2232540213603764 от dashakid1 25.02.2023 06:22

Question

Математика: Найдите корни уравнения 2 sin2 (3π / 2 – x) + 5 sin x = 4 на промежутке [0; π / 2].

dashakid1 · Answer

Синус ограничен: [-1;1]. Поэтому первое выражение не имеет решений.В заданном промежутке присутствует только один корень:...