По условию задачи каменщиков 5, значит частей тоже 5. Три части из пяти у каменщиков, которые израсходовали по 326 кирпичей, остальные две части у двух других каменщиков. Разница между этими частями одна пятая, которая равна:
326 * 3 = 978(кирпичей);
далее вычисляем, сколько всего было кирпичей:
978 * 5 = 4890.
ответ: вначале недели каменщики получили всего 4890 кирпичей.
№2:Решение
1) 1/6 + 1/8 = 8/48 + 6/48 = 14/48 = 7/24.
ответ: за 1 час автомобили приближаются к друг другу на 7/24 всего пути.
Тут нужно воспользоваться формулой Бернулли, описывающей вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события равна p, событие наступит ровно k раз.
Будем решать задачу от обратного. Найдем вероятность противоположного события, а именно: вероятность того, что неправильный ответ будет зафиксирован 0 или 1 раз.
Для такой задачи
Тогда вероятность того, что ответ будет зафиксирован 0 или 1 раз равна
Тогда вероятность того, что неправильный ответ появится хотя бы 2 раза:
Таким образом, можно сказать, что вероятность того, что детектор зафиксирует хотя бы 2 неправильных ответа, сильно близка к 1
№1:Решение
По условию задачи каменщиков 5, значит частей тоже 5. Три части из пяти у каменщиков, которые израсходовали по 326 кирпичей, остальные две части у двух других каменщиков. Разница между этими частями одна пятая, которая равна:
326 * 3 = 978(кирпичей);
далее вычисляем, сколько всего было кирпичей:
978 * 5 = 4890.
ответ: вначале недели каменщики получили всего 4890 кирпичей.
№2:Решение
1) 1/6 + 1/8 = 8/48 + 6/48 = 14/48 = 7/24.
ответ: за 1 час автомобили приближаются к друг другу на 7/24 всего пути.
№3:Решение
1) 48 : 3/4 = 36 (м) отрезали от веревки;
2) 48 – 36 = 12 (м).
ответ: веревка стала равна 12 метров.
0.99999999998134765625
Пошаговое объяснение:
Тут нужно воспользоваться формулой Бернулли, описывающей вероятность того, что в n независимых испытаниях, в каждом из которых вероятность наступления события равна p, событие наступит ровно k раз.
Будем решать задачу от обратного. Найдем вероятность противоположного события, а именно: вероятность того, что неправильный ответ будет зафиксирован 0 или 1 раз.
Для такой задачи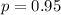
Тогда вероятность того, что ответ будет зафиксирован 0 или 1 раз равна
Тогда вероятность того, что неправильный ответ появится хотя бы 2 раза:
Таким образом, можно сказать, что вероятность того, что детектор зафиксирует хотя бы 2 неправильных ответа, сильно близка к 1