Найдите наибольшее число цветов, в которое можно раскрасить все натуральные числа так, что если числа a и b одного цвета (возможно, a=b), то число a+b того же цвета
опять будем менять знак, т.к. основание логарифма 1/3 < 1
свойства алгоритма применяемые в данном примере:
1)log(a)+log(b)=log(a*b)
2)a>0 и b>0
ОДЗ:
x-2>0 ----> x>2
12-x>0 ----> x<12
найдём дискриминант квадратного уравнения:
то, что дискриминант отрицательный нам говорит, что парабола не касается оси Ох, и т.к. коэффициент при x² >0, то ветви параболы направлены вверх(видно на рисунке), исходя из этого делаем выводы что данное квадратное уравнение положительно при любых х.
1) x≤2
2)x>3
3)2<x<12
Пошаговое объяснение:
1)
2)
меняем знак, т.к. основание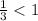
3)
опять будем менять знак, т.к. основание логарифма 1/3 < 1
свойства алгоритма применяемые в данном примере:
1)log(a)+log(b)=log(a*b)
2)a>0 и b>0
ОДЗ:
x-2>0 ----> x>2
12-x>0 ----> x<12
найдём дискриминант квадратного уравнения:
то, что дискриминант отрицательный нам говорит, что парабола не касается оси Ох, и т.к. коэффициент при x² >0, то ветви параболы направлены вверх(видно на рисунке), исходя из этого делаем выводы что данное квадратное уравнение положительно при любых х.
Включая ОДЗ, получаем ответ:
2<x<12(или x∈(2;12))
272544 ÷ (x + 68) = 4008;
Представим, что (х + 68) одно число и у нас пример деления. Чтобы найти неизвестный делитель, нужно делимое разделить на частное чисел.
Х + 68 = 272544 ÷ 4008;
Запишем частное чисел.
Х + 68 = 68;
Число 68 перенесем в другую часть уравнения, поменяем знак плюс на минус.
Х = 68 - 68;
Найдем разность чисел.
Х = 0;
Проверим уравнение. Поставим вместо неизвестного найденную цифру и вычислим как выражение.
272544 ÷ (68 + 68) = 4008;
Делаем сложение в скобке.
272544 ÷ 136 = 4008;
Найдем частное чисел.
4008 = 4008.
Пошаговое объяснение:
отметь как лучшее