3x²-18x+24=0 |:3
x²-6x+8=0
x₁= ∉ [-1;3]
x₂= ∈ [-1;3]
Получается, что:
у(наиб.)=y(2)=19
у(наим.)=y(-1)=-35
3x²-18x+24=0 |:3
x²-6x+8=0
x₁=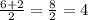
∉ [-1;3]
x₂=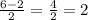
∈ [-1;3]
Получается, что:
у(наиб.)=y(2)=19
у(наим.)=y(-1)=-35