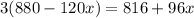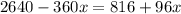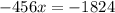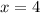Сумма всех углов равна 360°. Тогда мы можем найти 1 угол. Обозначим этот угол буквой α
α=360°-280°=80°. Это будет меньший угол параллелограмма, потому что он острый. У параллелограмма большим углом считается тупой угол. Но мы также знаем, что сумма прилежащих к одной стороне углов параллелограмма равна 180°. Это также можно доказать через параллельность прямых: если боковая сторона является секущей при параллельных прямых, то два соответствующих внутренних угла в сумме равны 180°. Итак, больший угол параллелограмма будет равен 180°-80°=100°
ответ: 1) В книге всего 320 страниц 2) через 4 дня во 2 складе станет в 3 раза больше тонн торфа чем в 1 складе
Пошаговое объяснение: 1) пусть общее число страниц в книге x тогда
1-й день - после чего осталось 2-й день - страниц от оставшегося кол-ва страниц то есть В 3-й день прочел 84 страницы найдем ту часть которую ему осталось прочитать на 3-й день то есть страниц всего в книге 320 2) В 1 складе 880 тонн торфа Во 2 складе 816 тонн торфа нам известно что из первого каждый день вывозят по 120 тонн в день а ; во второй каждый день привозят и нам сказано через сколько дней во втором складе станет в 3 раза больше торфа чем в первом пусть кол-во дней равно x и нам также известно что
100°
Пошаговое объяснение:
Сумма всех углов равна 360°. Тогда мы можем найти 1 угол. Обозначим этот угол буквой α
α=360°-280°=80°. Это будет меньший угол параллелограмма, потому что он острый. У параллелограмма большим углом считается тупой угол. Но мы также знаем, что сумма прилежащих к одной стороне углов параллелограмма равна 180°. Это также можно доказать через параллельность прямых: если боковая сторона является секущей при параллельных прямых, то два соответствующих внутренних угла в сумме равны 180°. Итак, больший угол параллелограмма будет равен 180°-80°=100°
ответ: 1) В книге всего 320 страниц 2) через 4 дня во 2 складе станет в 3 раза больше тонн торфа чем в 1 складе
Пошаговое объяснение: 1) пусть общее число страниц в книге x тогда
1-й день -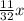 после чего осталось
после чего осталось 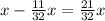 2-й день -
2-й день -  страниц от оставшегося кол-ва страниц то есть
страниц от оставшегося кол-ва страниц то есть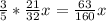 В 3-й день прочел 84 страницы найдем ту часть которую ему осталось прочитать на 3-й день то есть
В 3-й день прочел 84 страницы найдем ту часть которую ему осталось прочитать на 3-й день то есть 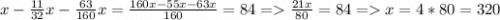 страниц всего в книге 320 2) В 1 складе 880 тонн торфа Во 2 складе 816 тонн торфа нам известно что из первого каждый день вывозят по 120 тонн в день а ; во второй каждый день привозят и нам сказано через сколько дней во втором складе станет в 3 раза больше торфа чем в первом пусть кол-во дней равно x и нам также известно что
страниц всего в книге 320 2) В 1 складе 880 тонн торфа Во 2 складе 816 тонн торфа нам известно что из первого каждый день вывозят по 120 тонн в день а ; во второй каждый день привозят и нам сказано через сколько дней во втором складе станет в 3 раза больше торфа чем в первом пусть кол-во дней равно x и нам также известно что