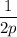при
Заметим, что для рассмотрения функции можно считать, что , так как в функцию входит в четной степени
Найдем производную:
Найдем точки, в которых производная равна нулю:
На промежутке с учетом уточнения такая точка одна:
Найдем точки, в которых производная не существует:
Равенство выполняется при , однако эта точка не попадает в заданный промежуток
Таким образом, нужно проверить наличие экстремума в точке .
Найдем знаки производной в точках и :
Значит:
Таким образом, при переходе через точку производная меняет знак с "плюса" на "минус". Значит, - точка максимума. Найдем значение максимума:
Поскольку заданный промежуток не отрезок, то проверим, что предел при стремлении к границам промежутка не больше полученного максимума:
Оба предела равны 0. Значит, - наибольшее значение функции на заданном промежутке.
ответ:
Заметим, что для рассмотрения функции можно считать, что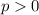 , так как в функцию
, так как в функцию 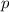 входит в четной степени
входит в четной степени
Найдем производную:
Найдем точки, в которых производная равна нулю:
На промежутке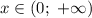 с учетом уточнения
с учетом уточнения 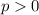 такая точка одна:
такая точка одна:
Найдем точки, в которых производная не существует:
Равенство выполняется при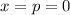 , однако эта точка не попадает в заданный промежуток
, однако эта точка не попадает в заданный промежуток 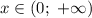
Таким образом, нужно проверить наличие экстремума в точке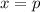 .
.
Найдем знаки производной в точках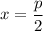 и
и 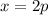 :
:
Значит:
при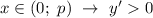
при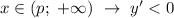
Таким образом, при переходе через точку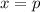 производная меняет знак с "плюса" на "минус". Значит,
производная меняет знак с "плюса" на "минус". Значит, 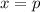 - точка максимума. Найдем значение максимума:
- точка максимума. Найдем значение максимума:
Поскольку заданный промежуток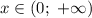 не отрезок, то проверим, что предел при стремлении
не отрезок, то проверим, что предел при стремлении  к границам промежутка не больше полученного максимума:
к границам промежутка не больше полученного максимума:
Оба предела равны 0. Значит,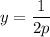 - наибольшее значение функции на заданном промежутке.
- наибольшее значение функции на заданном промежутке.
ответ: