y': 0++++++++|a|----------->
|a|>0: Наибольшее значение достигается в x=|a|, и имеет значение
|a|=0: Критических точек функция не имеет и убывает на всей области задания. - о наибольшем значении сказать ничего нельзя.
y': 0++++++++|a|----------->
|a|>0: Наибольшее значение достигается в x=|a|, и имеет значение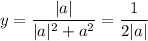
|a|=0: Критических точек функция не имеет и убывает на всей области задания.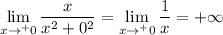 - о наибольшем значении сказать ничего нельзя.
- о наибольшем значении сказать ничего нельзя.