Пошаговое объяснение:
a) y = 2x - x², [-1;3]
Найдем производную f`(x) = 2 - 2x
Приравняем ее к нулю:
2 - 2x = 0; 2x = 2; x =1;
Теперь подставим x и крайние значения функций на отрезке [-1;3], это x = -1 и x = 3
y(-1) = 2 * (-1) - (-1)² = -2 -1 = -3
y(1) = 2 * 1 - 1² = 2 -1 = 1
y(3) = 2*3 - 3²= 6 -9 = -3, таким образом
y(максимальное) = y(1) = 1
y(минимальное) = y(-1) = y(3) = -3
б) y = x²+5x+6, [-4;3]
f`(x) = 2x + 5
2x + 5 = 0; 2x = -5
x = -2,5
y(-4) = (-4)²+5*(-4) + 6 = 16 - 20 + 6 = 2
y(3) = 3²+5*3+6 = 9 + 15 + 6 = 30
y(-2,5) =
y(максимальное)= y(3) = 30
y(минимальное) = y (-2,5) = - 0,25
Пошаговое объяснение:
a) y = 2x - x², [-1;3]
Найдем производную f`(x) = 2 - 2x
Приравняем ее к нулю:
2 - 2x = 0; 2x = 2; x =1;
Теперь подставим x и крайние значения функций на отрезке [-1;3], это x = -1 и x = 3
y(-1) = 2 * (-1) - (-1)² = -2 -1 = -3
y(1) = 2 * 1 - 1² = 2 -1 = 1
y(3) = 2*3 - 3²= 6 -9 = -3, таким образом
y(максимальное) = y(1) = 1
y(минимальное) = y(-1) = y(3) = -3
б) y = x²+5x+6, [-4;3]
f`(x) = 2x + 5
2x + 5 = 0; 2x = -5
x = -2,5
y(-4) = (-4)²+5*(-4) + 6 = 16 - 20 + 6 = 2
y(3) = 3²+5*3+6 = 9 + 15 + 6 = 30
y(-2,5) =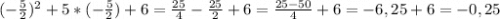
y(максимальное)= y(3) = 30
y(минимальное) = y (-2,5) = - 0,25