Найдите область определен ия функции: y=log√2(3x2-5x+2) Постройте график функции y=log2(x+1) Постройте график функции y=5x-2 Постройте график функции y=cos(x+π/6)
Знак неравенства меньше нуля, значит, нужно, чтоб квадратичная функция была расположена ниже оси абсцисс. Для этого требуется установить направление ветвь параболы. Очевидно, же что, когда ветви параболы направлены вниз и D<0(дискриминант меньше нуля), неравенство выполняется для всех действительных значения х.
Получаем решение системы неравенств . То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.
1)
Проверка:
0² - 25 · 0 = 0 25² - 25 · 25 = 0
0 - 0 = 0 25² - 25² = 0
0 = 0 0 = 0
2)
Проверка:
0² + 25 · 0 = 0 (-25)² + 25 · (-25) = 0
0 + 0 = 0 25² - 25² = 0
0 = 0 0 = 0
3)
Проверка:
0² - 1,7 · 0 = 0 1,7² - 1,7 · 1,7 = 0
0 - 0 = 0 1,7² - 1,7² = 0
0 = 0 0 = 0
Знак неравенства меньше нуля, значит, нужно, чтоб квадратичная функция была расположена ниже оси абсцисс. Для этого требуется установить направление ветвь параболы. Очевидно, же что, когда ветви параболы направлены вниз и D<0(дискриминант меньше нуля), неравенство выполняется для всех действительных значения х.
Получаем решение системы неравенств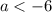
. То есть, при a ∈ (-∞;-6) неравенство (a+4)x²-2ax+2a-6<0 верно при всех действительных значения х. Наибольшее целое значение параметра а: а = -7.