Сначала расставим 3. Это можно сделать Для остальных букв остается 6 мест. Теперь на них расставим 2 Т. Это можно сделать Для остальных букв остается 4 места. И т.д. Тогда общее количество различных перестановок равно
a) В любой перестановке будет не более одного подслова «ТШ».
Подсчитаем все перестановки, его содержащие. Ш может стоять на любом месте со2 по 9ое => вариантов расстановки 8. Автоматически на предшествующее место ставим одну Т. Осталось расставить 3 Ф, 1 Т, 1 З, 1 М, 1 И. По аналогии с общим случаем, получаем общее число перестановок
Тогда ответ на этот пункт -
b) В любой перестановке будет не более одного подслова «ФЗ».
Подсчитаем все перестановки, его содержащие. З может стоять на любом месте со2 по 9ое => вариантов расстановки 8. Автоматически на предшествующее место ставим одну Ф. Осталось расставить 2 Ф, 2 Т, 1 Ш, 1 М, 1 И. По аналогии получаем общее число перестановок
Тогда ответ на этот пункт -
c) В любой перестановке будет не более двух подслов «ФТ».
В данном случае при аналогичном подходе мы будем учитывать слова с двумя «ФТ» 2 раза: один раз для "правого" подслова, и один для левого. Потому нужно будет отдельно найти число слов, содержащих 2 подслова.
Подсчитаем все перестановки. T может стоять на любом месте со2 по 9ое => вариантов расстановки 8. Автоматически на предшествующее место ставим одну Ф. Осталось расставить 2 Ф, 1 Т, 1 З, 1 Ш, 1 М, 1 И. По аналогии получаем общее число перестановок
Теперь для 2 подслов:
Сначала выставим "левое" подслово. Если справа осталось k>1 мест, то расставить на них подслово можно, очевидно Тогда общее число расстановки двух подслов равно
. Осталось расставить 1 Ф, 1 З, 1 Ш, 1 М, 1 И Тогда общее число перестановок
Для начала подсчитаем общее количество возможных комбинаций, которые могут выпасть. Согласно условию задачи дано 3 игральные кости, каждая из них имеет 6 граней, поэтому число всех комбинаций равно: 63 = 216 Теперь нужно подсчитать количество комбинаций, в которых выпадет ровно 7 очков. Перечислим их: 115, 124, 133, 142, 151,214, 223, 232, 241,313, 322, 331,412, 421,511Всего таких комбинаций получилось 15. Осталось лишь подсчитать вероятность выпадения одной из этих комбинаций. Для этого нужно поделить количество интересующих исходов на количество всех возможных исходов: P = 15 / 216 = 0.0694444... ≈ 0.07
ФЗФТШМФТИ - 3 Ф, 2 Т, 1 З, 1 Ш, 1 М, 1 И. 9 букв
Сначала расставим 3. Это можно сделать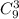 Для остальных букв остается 6 мест. Теперь на них расставим 2 Т. Это можно сделать
Для остальных букв остается 6 мест. Теперь на них расставим 2 Т. Это можно сделать 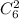 Для остальных букв остается 4 места. И т.д. Тогда общее количество различных перестановок равно
Для остальных букв остается 4 места. И т.д. Тогда общее количество различных перестановок равно 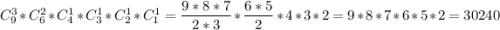
a) В любой перестановке будет не более одного подслова «ТШ».
Подсчитаем все перестановки, его содержащие. Ш может стоять на любом месте со2 по 9ое => вариантов расстановки 8. Автоматически на предшествующее место ставим одну Т. Осталось расставить 3 Ф, 1 Т, 1 З, 1 М, 1 И. По аналогии с общим случаем, получаем общее число перестановок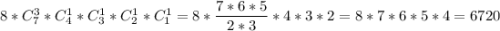
Тогда ответ на этот пункт -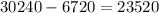
b) В любой перестановке будет не более одного подслова «ФЗ».
Подсчитаем все перестановки, его содержащие. З может стоять на любом месте со2 по 9ое => вариантов расстановки 8. Автоматически на предшествующее место ставим одну Ф. Осталось расставить 2 Ф, 2 Т, 1 Ш, 1 М, 1 И. По аналогии получаем общее число перестановок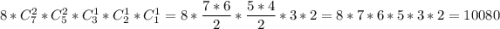
Тогда ответ на этот пункт -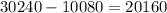
c) В любой перестановке будет не более двух подслов «ФТ».
В данном случае при аналогичном подходе мы будем учитывать слова с двумя «ФТ» 2 раза: один раз для "правого" подслова, и один для левого. Потому нужно будет отдельно найти число слов, содержащих 2 подслова.
Подсчитаем все перестановки. T может стоять на любом месте со2 по 9ое => вариантов расстановки 8. Автоматически на предшествующее место ставим одну Ф. Осталось расставить 2 Ф, 1 Т, 1 З, 1 Ш, 1 М, 1 И. По аналогии получаем общее число перестановок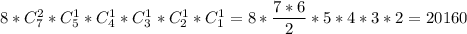
Теперь для 2 подслов:
Сначала выставим "левое" подслово. Если справа осталось k>1 мест, то расставить на них подслово можно, очевидно Тогда общее число расстановки двух подслов равно
Тогда ответ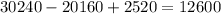
63 = 216 Теперь нужно подсчитать количество комбинаций, в которых выпадет ровно 7 очков. Перечислим их:
115, 124, 133, 142, 151,214, 223, 232, 241,313, 322, 331,412, 421,511Всего таких комбинаций получилось 15. Осталось лишь подсчитать вероятность выпадения одной из этих комбинаций. Для этого нужно поделить количество интересующих исходов на количество всех возможных исходов:
P = 15 / 216 = 0.0694444... ≈ 0.07